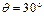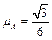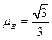1、简答题  如图所示，在倾角、足够长的斜面上分别固定着两个物体A．B，相距L=0.2m，它们的质量mA=mB=1kg，与斜面间的动摩擦因数分别为和．在t=0时刻同时撤去固定两物体的外力后，A物体将沿斜面向下运动，并与B物体发生连续碰撞(碰撞时间极短，忽略不计)，每次碰后两物体交换速度．g取10m/s2．求：
（1）A与B第一次碰后瞬时B的速率？
（2）从A开始运动到两物体第二次相碰经历多长时间？
（3）至第n次碰撞时A、B两物体通过的路程分别是多少？

参考答案：（1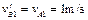）?（2）1.2s?（3）[0.2+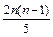]m

本题解析：(1) A物体沿斜面下滑时有
　　　　　　　　
∴
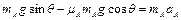
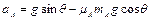
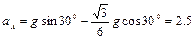m/s2　　　　
B物体沿斜面下滑时有

∴
　　　　　　　
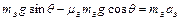
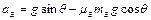
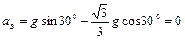
综上分析可知，撤去固定A、B的外力后，物体B恰好静止于斜面上，物体A将沿斜面向下做匀加速直线运动．?
由运动学公式得A与B第一次碰撞前的速度?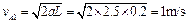
由于AB碰撞后交换速度，故AB第一次碰后瞬时，B的速率?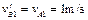
(2)从AB开始运动到第一次碰撞用时?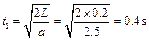
两物体相碰后，A物体的速度变为零，以后再做匀加速运动，而B物体将以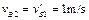的速度沿斜面向下做匀速直线运动．?
设再经t2时间相碰，则有?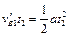
解之可得t2="0.8s?" 　　　　　　
故从A开始运动到两物体第二次相碰，共经历时间t=t1+t2="0.4+0.8=1.2s?"
（3）从第2次碰撞开始，每次A物体运动到与B物体碰撞时，速度增加量均为Δv=at2=2.5×0.8m/s=2m/s，由于碰后速度交换，因而碰后B物体的速度为：
第一次碰后： vB1=1m/s
第二次碰后： vB2=2m/s
第三次碰后： vB3=3m/s
……
第n次碰后： vBn=nm/s
每段时间内，B物体都做匀速直线运动，则第n次碰前所运动的距离为
sB=[1+2+3+……+（n-1）]×t2=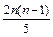?m? (n=1，2，3，…，n-1)
A物体比B物体多运动L长度，则
sA = L+sB=[0.2+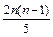]m

本题难度：一般

2、计算题  物体在倾角为θ的斜面上滑动，则在下列两种情况下，物体加速度为多大？
（1）斜面是光滑的；
（2）斜面是粗糙的，且与物体间动摩擦因数为μ

参考答案：（1）a1=gsinθ（2）a2=g（sinθ－μcosθ）， a3=g（sinθ+μcosθ）

本题解析：
【错解分析】错解：对物体在倾角为θ的斜面上滑动，理解为物体在倾角为θ的斜面上向下滑动，导致漏去分析和考虑物体在倾角为θ的斜面上向上滑动的情况。
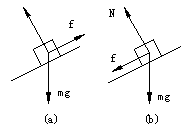
【正解】（1）对于光滑斜面，无论物体沿斜面向下滑或是沿斜面向上滑，其受力情况均可由图所示，建立适当的坐标系后便可列出运动方程
mgsinθ=ma1，
得? a1=gsinθ.
（2）对于粗糙斜面，物体滑动时还将受动摩擦力作用，只是物体向下滑时动摩擦力方向沿斜面斜向上；物体向上滑时动摩擦力方向沿斜面斜向下，受力图分别如图中（a）、（b）所示，建立适当的坐标系后便可分别列出方程组

和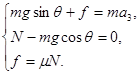
由此便可分别解得
a2=g（sinθ－μcosθ），
a3=g（sinθ+μcosθ）

本题难度：一般

3、选择题  由一根内壁光滑的玻璃管构成一个直角三角形处于竖直平面内，倾斜角为θ=37°，让两个相同的小球同时从顶端A静止开始出发．一个球沿AC做加速度大小为a=gsin37°的匀加速运动至C，到达C所用的时间为t1，另一个球竖直自由下落经过B后匀速运动到达C，所用的时间为t2，在转弯处有个极小的光滑圆弧，可确保小球转弯时速度大小不变，且转弯时间可以忽略不计．（其中sin37°=0.6，cos37°=0.8）．比较t1与t2的关系（　　）
A．t1＜t2
B．t1=t2
C．t1＞t2
D．条件不够无法确定