1、计算题 如图所示,匀强磁场宽L="30" cm,B=3.34×10-3 T,方向垂直纸面向里.设一质子以v=1.6×105 m/s 的速度垂直于磁场B的方向从小孔C射入磁场,然后打到照相底片上的A点. 试求:

(1)质子在磁场中运动的轨道半径r;
(2)A点距入射线方向上的O点的距离H;
(3)质子从C孔射入到A点所需的时间t.(质子的质量为1.67×10-27 kg;质子的电荷量为1.6×10-19 C)
参考答案:(1)0.5m;(2)0.1m;(3)2×10-6s
本题解析:(1)根据公式得:qvB=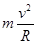
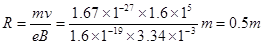 ,
,
(2)由平面几何关系得:R2=L2+(R-H)2 得H=0.1m
(3)sinθ= 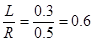 θ=37°
θ=37°
质子在磁场中转动的角度为37°,则运动时间为:
 .
.
考点:带电粒子在匀强磁场中的运动
本题难度:一般
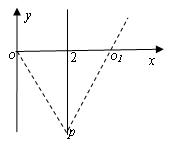
2、计算题 如图所示,宽x=2cm的有界匀强磁场的纵向范围足够大,磁感应强度的方向垂直纸面向内,大小为0.01T。现有一群比荷q/m=4×107C/kg的正粒子,从O点以相同的速率2×104m/s沿纸面不同方向进入磁场,粒子重量忽略不计(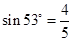 )。求:
)。求:
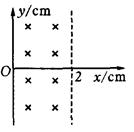
(1)粒子在磁场中做圆周运动的半径;
(2)所有打在y轴上的粒子在磁场中运动的最长时间;
(3)打在分界线x=2cm上粒子的分布范围.
参考答案:(1)0.05m?(2)4.62×10-6s?(3)x轴下方0.04m到x轴上方0.04m之间均有粒子
本题解析:(1)根据粒子在磁场中运动是洛伦兹力提供向心力可得: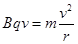 ,求得r=0.05m;
,求得r=0.05m;
(2)粒子做圆周运动的周期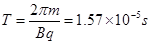 ,设粒子运动轨迹的圆心角为θ,则粒子在磁场中运动的时间
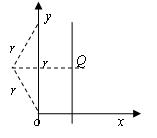
,设粒子运动轨迹的圆心角为θ,则粒子在磁场中运动的时间 ,由题意知,当粒子的轨迹与磁场右边界相切时,粒子打在y轴上,轨迹的圆心角最大,运动的时间最长,如图所示,根据几何关系可求圆心角为106o,代入可求运动时间t=4.62×10-6s;
,由题意知,当粒子的轨迹与磁场右边界相切时,粒子打在y轴上,轨迹的圆心角最大,运动的时间最长,如图所示,根据几何关系可求圆心角为106o,代入可求运动时间t=4.62×10-6s;
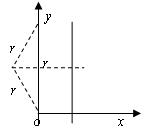
(3)由题意知,当粒子的速度沿y轴负方向时粒子从p点离开磁场,且p点为粒子打在分界线x=2cm上的最低点,如图所示,由几何关系可求p点到x轴的距离为0.04m;当粒子轨迹与分界线x=2cm相切时,切点Q为粒子在分界线x=2cm上的最高点,如图所示根据几何关系可求Q到x轴的距离为0.04m,所以打在分界线x=2cm上粒子的分布在x轴下方0.04m到x轴上方0.04m的范围内。
本题难度:简单
3、选择题 如图所示,两个半径相同的半圆形光滑轨道置于竖直平面内,左右两端等高,分别处于沿水平方向的匀强磁场和匀强电场中。两个相同的带正电小球同时从两轨道左端最高点由静止释放。M、N为轨道最低点,则下列说法中正确的是
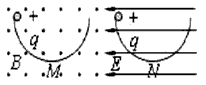
[? ]
A.两个小球到达轨道最低点的速度vM>vN
B.两个小球第一次经过轨道最低点时对轨道的压力FM<FN
C.小球第一次到达M点的时间大于小球第一次到达N点的时间
D.在磁场中小球能到达轨道的另一端最高处,在电场中小球仍能到达轨道另一端最高处
参考答案:A
本题解析:
本题难度:一般
4、选择题 如图所示,一个质量为m,电荷量为q的带电粒子(重力不计),沿着垂直磁场边界方向,在a点射入磁感强度为B、宽度为d的匀强磁场,粒子速度方向和B垂直,粒子从b 点射出磁场,出射点与入射点a的竖直距离为.则.以下说法正确的是:( )

A.此粒子一定带负电;
B.粒子经过磁场时动能不变
C.带电粒子射入磁场时的速率为
D.粒子做圆周运动的轨迹半径等于
参考答案:ABC
本题解析:根据粒子的偏转,根据左手定则,可知粒子带负电,A对;洛仑兹力与速度垂直不做功,所以粒子动能不变,B对;由运动轨迹,连接ab,做ab的中垂线与左边界交于一点即为圆心,根据几何关系可知: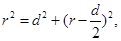 解得r=3d/4,由
解得r=3d/4,由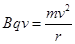 ,解得v=,所以C对;D错。
,解得v=,所以C对;D错。
本题难度:简单
5、简答题 如图所示,PQ为一块长为L、水平固定放置的绝缘平板,整个空间存在着水平向左的匀强电场,板的右半部分存在着垂直于纸面向里的有界匀强磁场.一质量为m、带电荷量为q的物体,从板左端P由静止开始做匀加速运动,进入磁场后恰好做匀速直线运动,碰到右端带控制开关K的挡板后被弹回,且电场立即被撤消,物体在磁场中仍做匀速运动,离开磁场后又做匀减速运动,最后停在C点,已知PC=
,物体与板间动摩擦间数为μ,求:
(1)物体带何种电荷?
(2)物体与板碰撞前后的速度v1和v2
(3)电场强度E和磁感应强度B各多大?

参考答案:解(1)物体带负电;
(2)因碰前匀速,有:Qe=μ(qv1B+mg).
碰后先匀速有:qv2B=mg
再减速最后停止在C点,从P到进入磁场的过程中,由动能定理:qEl2-μmgl2=12mv21
从出磁场到C点,由动能定理:-μmgl4=0-12mv22
解得:v1=
本题解析:
本题难度:一般