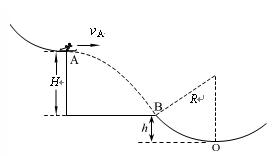
1、计算题  如图所示，一滑雪运动员质量m＝60kg，经过一段加速滑行后从A点以vA＝10m/s的初速度水平飞出，恰能落到B点．在B点速度方向（速度大小不变）发生改变后进入半径R＝20m的竖直圆弧轨道BO，并沿轨道下滑．已知在最低点O时运动员对轨道的压力为2400N．A与B、B与O的高度差分别为H＝20m、h＝8m．不计空气阻力，取g＝10m/s2，求：
（1）AB间的水平距离．
（2）运动员在BO段运动时克服阻力做的功．

参考答案：

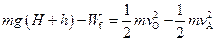?（4分）
解得：?（2分）
或：?（1分）
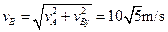故?（1分）
设由B到O克服摩擦力做功为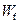，由动能定理，有
?（2分）
解得：?（2分）

本题解析：略

本题难度：一般

2、简答题  OA杆是机器带动绕其轴线旋转的竖直杆，细绳的一端固定在杆的A点，另一端系一质量m="1" kg的小球，绳长为L="1" m.开始小球绕轴线在水平面内做匀速圆周运动，细绳与竖直杆的夹角为θ1=30°.现使机器转速加大，使小球在另一水平面内做稳定的匀速圆周运动时，细绳与竖直杆的夹角为θ2=60°.求此过程中机器对小球所做的功.（取g="10" m/s2）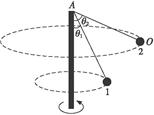

参考答案：W机≈9.72 J

本题解析：（1）设摆角为θ时，小球角速度为ω,绳中张力为T，则

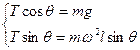
ω2=.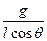
（2）小球动能
Ek=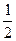mv2=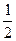mω2(lsinθ)2=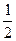mgl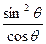
（3）由状态1到2：对小球，由动能定理
WG+W机=ΔEk
-mgl(cosθ1-cosθ2)+W机=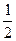mgl(-)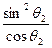
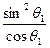则W机=mgl(cosθ1-cosθ2)+
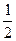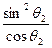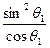mgl(-)=10×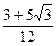
J=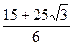?J≈9.72 J.

本题难度：一般

3、计算题  如图所示，ABCD为竖立放在场强为E＝104 V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的部分是半径为R的半圆环，轨道的水平部分与半圆环相切，A为水平轨道上的一点，而且＝R＝0.2 m．把一质量m＝0.1 kg、带电量q＝10－4 C的小球，放在水平轨道的A点由静止开始释放后，在轨道的内侧运动．(g取10 m/s2)求：

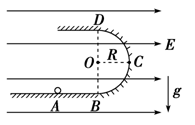
小题1:它到达C点时的速度是多大？
小题2:它到B达点时对轨道压力是多大？
小题3:若让小球安全通过D点，还从A点释放小球场强应该变为多大？

参考答案：
小题1:2 m/s
小题2:3 N
小题3:E≥2.5 *104m

本题解析：略

本题难度：简单

4、填空题  如图所示，轻杆长1m，其两端各连接质量为1kg的小球，杆可绕距B端0.2m处的轴O在竖直面内转动，控制外部环境使A球转到最低点时速度大小为4m/s，此时B球的速度大小为         ，轴与杆之间的作用力大小为         。（g=10m/s2）

参考答案： 1m/s ； 35N 

本题解析：A球的角速度为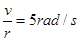，AB角速度相同，B的线速度为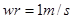，设B受到杆的作用力为F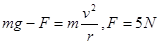，，以A球为研究对象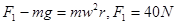，轴与杆之间的作用力大小为35N

本题难度：一般

5、选择题  甲乙物体都做匀速圆周运动，甲球的轨道半径是乙球的2倍，在1min内甲球转动次数是乙球的1/2，则两球的加速度之比是：
A．1∶1
B．1∶2
C．2∶3
D．3∶2

参考答案：B

本题解析：
分析：本题考察了对圆周运动中的基本公式的掌握情况，可以直接利用向心加速度的表达式进行求解。
解答：根据向心加速度表达式得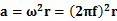：?再由题中所给转速、半径关系，联立可得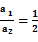：，故ACD错误，B正确。

本题难度：简单