1、选择题  如图所示表示甲、乙两运动物体相对同一原点的位移—时间图象，下面说法中正确的是(? )

A．甲和乙都做匀速直线运动
B．甲、乙运动的出发点相距x0
C．甲、乙两物体在x0/2处相遇
D．乙比甲早出发t1的时间

参考答案：ABC

本题解析：位移-时间图象反映物体的位置坐标随时间的变化规律；图象中，倾斜的直线表示匀速直线运动；向上倾斜时速度为正，向下倾斜使速度为负；交点表示两物体相遇；初始位置的坐标即为两物体出发时的距离．A、x-t图象的斜率等于物体运动的速度，由图可知两图象的斜率保持不变，故运动的速度不变，即两物体都做匀速直线运动．故A正确；
B、由图可知乙从原点出发，甲从距原点x0处出发．故两物体的出发点相距x0．故B正确；
C、由图象可知在甲、乙两物体同时到达x0/2，即相遇，故C正确；
D、由图象可知甲从 t=0时刻开始运动，而乙从t1时刻开始运动，故甲比乙早出发，故D错误；
故选ABC．
点评：本题关键要明确位移时间图象的含义，在位移-时间图象中，倾斜的直线表示物体的位置坐标随时间均匀变化，物体做匀速直线运动；还要明确交点（两图象的交点、与坐标轴的交点）的意义．

本题难度：一般

2、选择题  甲、乙两车从同一地点出发，向同一方向行驶，它们的x-t图象如图所示，则由图可看出（?）

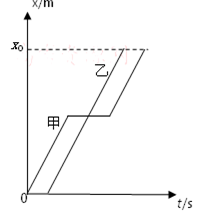
A．乙比甲先出发，甲比乙先到达距出发点x0处
B．甲比乙先出发，乙比甲先到达距出发点x0处
C．两车的平均速度相同
D．两车行驶时的速度相同

参考答案：BD

本题解析：从图中我们可知甲比乙先出发，而乙比甲先达到距离出发点x0处，A错误B正确。因为两车发生的位移相等，甲花费的时间比乙的多，故根据公式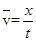可得两车的平均速度相等，但两车在行驶时的速度不一样，甲在某段时间内处于静止状态，而乙一直匀速行驶，D错误。

本题难度：一般

3、选择题  a、b两车在两条平行的直车道上同方向行驶，它们的v－t图象如图7所示。在 t=5s时，它们第一次相遇。关于两车之间的关系，下列说法正确的是

A．t=0s，a车在前
B．t=10s，两车第二次相遇
C．t=15s，两车第二次相遇
D．t=20s，两车第二次相遇

参考答案：C

本题解析：根据在 t=5s时，它们第一次相遇可知，t=0s，a车在后，选项A错误；t=10s，两车速度相等，a车在前，选项B错误；t=15s，两车第二次相遇，选项C正确D错误。

本题难度：简单

4、计算题  一辆值勤的警车停在平直公路边，当警员发现从他旁边以v＝8 m/s的速度匀速驶过的货车有违章行为时，决定前去追赶，经2.5 s，警车发动起来，以加速度a＝2 m/s2做匀加速运动，试问：
(1)警车发动起来后要多长的时间才能追上违章的货车？
(2)在警车追上货车之前，两车间的最大距离是多少？
(3)若警车的最大速度是12 m/s，则警车发动起来后要多长的时间才能追上违章的货车？

参考答案：(1)10 s　(2)36 m　(3)14 s

本题解析：Δs＝Δt·v＝2.5×8 m＝20 m.
(1)设警车发动起来后要时间t才能追上违章的货车，则?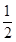at2－vt＝Δs
解得t＝10 s或t＝－2 s(舍去)．
(2)在警车追上货车之前，两车速度相等时，两车间的距离最大，设警车发动起来后经时间t′两车速度相等，两车间的距离最大为sm，则：t′＝＝4 s
sm＝Δx＋v·t′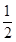－at′2＝(20＋8×4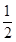－×2×42) m＝36 m.
(3)若警车的最大速度是12 m/s，则警车发动起来后加速的时间：t0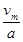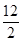＝＝s＝6 s
设警车发动起来后经过时间t″追上违章的货车，则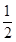：a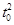＋vm(t″－t0)－vt″＝Δx
解得t″＝14
点评：做分析追击相遇问题的时候，方法大致分为两种，一种是物理分析法：即通过对物理情景和物理过程的分析找到临界状态和临界条件，然后列出等式求解，，另一种是数学方法，因为在匀变速直线运动的位移表达式中有时间的二次方，我们可列出方程，利用二次函数求极值，有时也可借助v-t图像解题

本题难度：一般

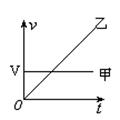
5、选择题  汽车甲沿平直的公路以速度v作匀速直线运动，当它路过某处的同时，该处一辆汽车乙开始作初速度为零的匀加速直线运动，去追赶甲车，根据上述条件，（?）

A．可求出乙车追上甲车时乙车的速度
B．可求出乙车追上甲车时乙车所走的路程
C．可求出乙车追上甲车所用的时间
D．可求出追上前，两车相距最远时，乙车的速度

参考答案：AD

本题解析：追上时位移相等，如图面积相等故v乙=2v甲?
又因为追上前当两车速度相等时相距最远，所以此时V乙=V

本题难度：一般