1、计算题  如图，线圈的面积是0.05m2，共100匝，线圈总电阻为1Ω，外接电阻R=9Ω，匀强磁场的磁感应强度为B=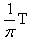，当线圈以300r/min的转速匀速旋转时，求：
（1）若从线圈处于中性面开始计时，写出线圈中感应电动势的瞬时值表达式；
（2）线圈转了时电动势的瞬时值多大？
（3）电路中电压表、电流表的示数各是多少？

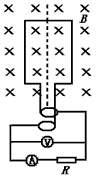
参考答案：解：（1）

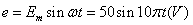
（2）
（3）
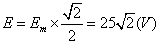
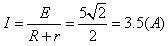，电流表读数为3.5A
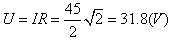，电压表读数为31.8V

本题解析：

本题难度：一般

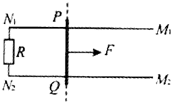
2、简答题  如图所示，M1N1N2M2是位于光滑水平桌面上的刚性U型金属导轨，导轨中接有阻值为R的电阻，它们的质量为m0．导轨的两条轨道间的距离为l，PQ是质量为m的金属杆，可在轨道上滑动，滑动时保持与轨道垂直，杆与轨道的接触是粗糙的，杆与导轨的电阻均不计．初始时，杆PQ于图中的虚线处，虚线的右侧为一匀强磁场区域，磁场方向垂直于桌面，磁感应强度的大小为B．现有一位于导轨平面内的与轨道平行的恒力F作用于PQ上，使之从静止开始在轨道上向右作加速运动．已知经过时间t，PQ离开虚线的距离为x，此时通过电阻的电流为I0，导轨向右移动的距离为x0（导轨的N1N2部分尚未进入磁场区域）．求：
（1）杆受到摩擦力的大小？
（2）经过时间t，杆速度的大小v为多少？
（3）在此过程中电阻所消耗的能量．（不考虑回路的自感）．

参考答案：（1）因U型导轨在滑动摩擦力作用下做匀加速度直线运动，
则有：Fμ=m0a
而：a=2x0t2
所以：Fμ=2m0x0t2
根据牛顿第三定律，杆受到的摩擦力大小：F′μ=Fμ=2m0x0t2
（2）设经过时间t杆的速度为v，则杆与导轨构成的回路中的感应电动势：
E=Blv
根据题意，此时回路中的感应电流：
I0=ER
得：v=I0RBl
（3）杆的合力做功等于杆所增加的动能，即：
WF+WF安+WFμ=12mv2
WF为恒力F对杆做的功：WF=Fx
WFμ为摩擦力对杆做的功：WFμ=-Fμ?x
杆克服安培力做的杆等于电阻所消耗的能量，若以ER表示电阻所消耗的能量，
则有-WF安=ER
电阻所消耗的能量：ER=(F-2m0x0t2)x-12mI20R2B2l2
答：（1）杆受到摩擦力的大小2m0x0t2；
（2）经过时间t，杆速度的大小v为I0RBl；
（3）在此过程中电阻所消耗的能量ER=(F-2m0x0t2)x-12mI20R2B2l2．

本题解析：

本题难度：一般

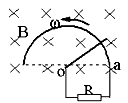
3、选择题  如图所示，在磁感强度为B的匀强磁场中，有半径为r的光滑半圆形导体框架，OC为一能绕O在框架上滑动的导体棒，OC之间连一个电阻R，导体框架与导体棒的电阻均不计，若要使OC能以角速度ω匀速转动，则外力做功的功率是：

[? ]
A．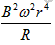
B．
C．
D．

参考答案：C

本题解析：

本题难度：一般

4、选择题  如图所示为闭合电路中的一部分导体ab在磁场中做切割磁感线运动的情景，其中能产生由a到b的感应电流的是（　　）
A．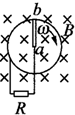
B．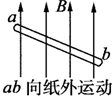
C．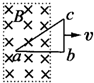
D．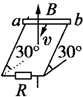

参考答案：A

本题解析：

本题难度：简单

5、选择题  如图所示，水平面上固定有间距为1m的平行光滑导轨，磁感应强度为1T的匀强磁场方向竖直向下。导体棒ab的质量为1kg、电阻为2Ω；cd的质量为2kg、电阻为1Ω。开始时ab静止，cd棒以6m/s的初速度向右运动，经过t＝4s，棒ab、cd的运动开始稳定。运动过程中两棒始终与导轨垂直，且与导轨接触良好，其它电阻不计。则

[? ]

参考答案：BC

本题解析：

本题难度：一般