1、计算题 (14分)一足够长水平浅色传送带以V0匀速运动,现将一可视为质点的小煤块轻放在其上方,已知煤块与传送带间的动摩擦因数为μ。经过一定时间后达到共同速度。令传送带突然停下,以后不再运动,到最后煤块也停下。已知重力加速度为g。求:(1)煤块第一次达到与传送带相对静止所用的时间;(2)煤块在传送带上划出的痕迹长度。
参考答案:(1)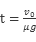 ?(2)
?(2)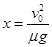
本题解析:(1)煤块的加速度a=μg?(3分)
达到V0所用时间t= ?(3分)
?(3分)
(2)在煤块与传送带达到共同速度的过程中,
传送带运动的距离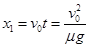 ?(1分)
?(1分)
煤块运动的距离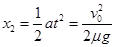 ?(1分)
?(1分)
此过程中划出的痕迹长度为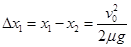 (2分)
(2分)
传送带突然停下后,煤块继续做匀减速运动,直至停下,这一过程煤块向前运动的距离为 ?(2分)
?(2分)
考虑重叠部分,最终划出的痕迹长度为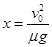 ?(2分)
?(2分)
本题难度:一般
2、计算题 如图所示,某滑道由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(不考虑能量损失),其中轨道AB段是光滑的,水平轨道BC的长度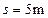 ,轨道CD足够长且倾角
,轨道CD足够长且倾角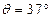 ,A点离轨道BC的高度为
,A点离轨道BC的高度为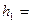 4.30m。现让质量为m的小滑块自A点由静止释放,已知小滑块与轨道BC、CD间的动摩擦因数都为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8。试求:
4.30m。现让质量为m的小滑块自A点由静止释放,已知小滑块与轨道BC、CD间的动摩擦因数都为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8。试求:
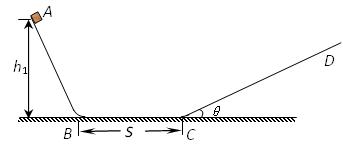
小题1:小滑块第一次到达C点时的速度大小
小题2:小滑块第一次和第二次经过C点的时间间隔
小题3:小滑块最终静止的位置距B点的距离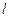
参考答案:
小题1: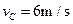
小题2: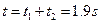
小题3: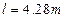
本题解析:(1)小物块第一次从A到C的过程中,由动能定理得
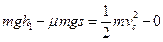 ?
?
将 、s、
、s、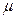 、g代入得:
、g代入得: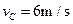 ?(4分)
?(4分)
(2)第一次冲上CD轨道上升的高度最大,上升过程的加速度大小为

上升的时间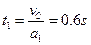 ?(2分)
?(2分)
则沿斜面上升的距离最大值为
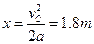 ?
?
返回时小滑块做匀加速运动,加速度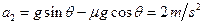
从最高点返回到C点所用的时间
 ?(2分)
?(2分)
故小滑块第一次和第二次经过C点的时间间隔
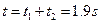 ?(2分)
?(2分)
(3)小球返回到C点的速度满足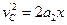
从C点向左的过程,由动能定理得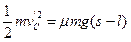
带入数字解得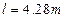 ?(4分)
?(4分)
本题难度:一般
3、简答题 一辆沿平直路面行驶的汽车,速度为10m/s.刹车后获得加速度的大小是4m/s2,求:
(1)刹车后3s末的速度;
(2)刹车后5s内的位移.
参考答案:(1)汽车刹车所用的时间为t0=v0a=104=2.5s
因为3s>2.5s,所以此时汽车已经停止运动,故速度为0
(2)因为5s>2.5s,所以此时汽车已经停止运动,
由x=v0t+12at2
解得:x=12.5m
答:(1)刹车后3s末的速度为0;
(2)刹车后5s内的位移为12.5m.
本题解析:
本题难度:一般
4、简答题 一辆汽车以36km/h的速度匀速行驶10s,然后又以1.5m/s2的加速度匀加速行驶10s.求:
(1)汽车在20s内的位移;
(2)汽车在15s末的瞬时速度;
(3)汽车在20s内的平均速度.
参考答案:汽车的初速度:v0=36km/h=10m/s
(1)汽车在20s内的位移分为匀速运动位移和匀加速运动位移:
前10s内匀速运动的位移x1=v0t=10×10m=100m
后10s内做匀加速运动的位移:x2=v0t+12at2=10×10+12×1.5×102m=175m
故汽车在前20s内的总位移:x=x1+x2=100+175m=275m
(2)由题意知汽车运动前10s做匀速运动,故15s末是汽车做匀加速运动5s末的瞬时速度,根据速度时间关系有:
v1=v0+at=10+1.5×5m/s=17.5m/s
(3)根据平均速度公式,汽车在前20s内的平均速度:
.v=xt=27520m/s=13.75m/s
答:(1)汽车在20s内的位移为275m;
(2)汽车在15s末的瞬时速度为17.5m/s;
(3)汽车在20s内的平均速度为13.75m/s.
本题解析:
本题难度:一般
5、选择题 汽车刹车的运动可视为匀减速直线运动,已知某辆汽车经过8s的时间速度减为零,最后2s内的位移是1m,则汽车减速过程的总位移是
A.8m
B.10m
C.16m
D.4m
参考答案:C
本题解析:分析:本题可以采用逆向思维求解,减速到0的匀减速直线运动可看成反向初速度为0的匀加速直线运动来处理,根据初速度为0的匀加速直线运动规律,可以方便解得.
解答:本题采用逆向思维,减速到0的匀减速直线运动的规律可看成初速度为0的匀加速直线运动
根据初速度为0的匀加速直线运动在从0开始连续相等时间内的位移比为:1:4:9:16
∵初速度为0的匀加速直线运动在前2s内的位移为1m
∴初速度为0的匀加速直线运动前8s内的位移为16m
所以匀减速运动8s内的位移等于初速度为0的匀加速直线运动8s内的位移即x=16m.
故选C.
点评:本题采用逆向思维,利用初速度为0的匀加速直线运动的规律求解.
本题难度:困难