1、简答题  一个小球作竖直上抛运动,经过时间t1上升到位置x1,经过时间t2上升到位置x2,小球上升到最高点后下落到位置x2的时间为t3,继续下落到位置x1的时间为t4.
求证重力加速度g=8(x2-x1)/[(t4-t1)2-(t3-t2)2].

2、计算题  如图所示，水平地面上有一个坑，其竖直截面为半圆。ab为沿水平方向的直径。若在a点以初速度v0沿ab方向抛出一小球，小球会击中坑壁上的c点。已知c点与水平地面的距离为圆半径的一半，求圆的半径。

3、简答题  如图所示，滑雪运动员以一定的速度从一平台的O点水平飞出，落地点A到飞出点O的距离OA=27m，山坡与水平面的夹角θ=37°．不计空气阻力．（已知sin37°=0.6，cos37°=0.8）求：
（1）运动员在空中运动的时间；
（2）运动员从O点飞出时的初速度．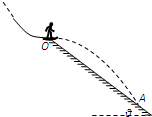

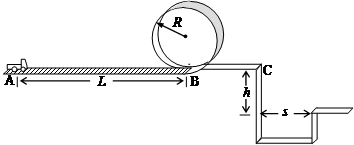
4、简答题  某校物理兴趣小组决定举行遥控赛车比赛．比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在光滑平直轨道上运动到C点，并能越过壕沟．已知赛车质量m=0.1kg，通电后以额定功率P=1.5w工作，进入竖直轨道前受到阻力恒为0.3N，随后在运动中受到的阻力均可不记．图中L=10.00m，R=0.32m，h=1.25m，S=2.50m．问：要使赛车完成比赛，电动机至少工作多长时间？（取g=10m/s2?）

5、简答题  [物理]
如图所示，摩托车做腾跃特技表演，以1m/s的初速度沿曲面冲上高0.8m顶部水平的高台，若摩托车冲上高台的过程中始终以额定功率1.8kW行驶，经过1.2s到达平台顶部．然后关闭发动机，离开平台，落至地面时，恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道，并沿轨道下滑，A、B为圆弧两端点，其连线水平，已知圆弧半径为R=1.0m，已知人和车的总质量为180kg，特技表演的全过程中不计一切阻力．则：（计算中取g=10m/s2，sin53°=0.8，cos53°=0.6）
（1）求人和车从顶部平台飞出的水平距离s；
（2）人和车运动到圆弧轨道最低点O时对轨轨道的压力．