1、选择题  宇航员在地球表面上滑得一单摆的振动周期为2s，若他将这一单摆带到某星球表面上，测得其振动周期为4s，忽略空气阻力，已知该星球的半径与地球半径之比为R星：R地=1：4，设地球表面重力加速度为g，星球表面的重力加速度为g"，地球质量为M地，星球质量为M星，则（　　）
A．g"：g=1：2
B．g"：g=4：1
C．M星：M地=1：16
D．M星：M地=1：64

参考答案：由单摆的周期公式：T=2π

本题解析：

本题难度：简单

2、简答题  英国某媒体推测：在2020年之前人类有望登上火星，而登上火星的第一人很可能是中国人．假如你有幸成为人类登陆火星的第一人，乘坐我国自行研制的代表世界领先水平的神舟x号宇宙飞船，通过长途旅行终于亲眼目睹了美丽的火星．为了熟悉火星的环境，你乘坐的x号宇宙飞船绕火星做匀速圆周运动，离火星表面高度为H，飞行了n圈，测得所用的时间为t，已知火星半径R，试求火星表面重力加速度g．

参考答案：根据万有引力提供向心力，有GMm(R+H)2=m(R+H)(2πT)2? ①
? T=tn? ②
根据万有引力等于重力，有GMmR2=mg? ③
联立①②③得，g=4n2π2(R+H)3R2t2
故火星表面的重力加速度g=4n2π2(R+H)3R2t2．

本题解析：

本题难度：一般

3、计算题  两颗靠的较近的天体称为双星，它们以两者的连线上某点为圆心做匀速圆周运动，而不会由于万有引力作用，使它们吸在一起（不考虑其他天体对它们的影响），已知两天体质量分别为m1和m2，相距为L，求它们运转的角速度。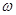

参考答案：ω=√G(m1+m2)/L3

本题解析：他们之间的相互作用力充当向心力，所以有：m1ω2r1=Gm1m2/L2（1）
m2ω2r2=Gm1m2/L2（2）
r1+r2= L（3）
联立三式可得ω=√G(m1+m2)/L3
点评：“双星”是万有引力部分常见的题型，关键抓住“双星”的条件：角速度相同、周期相同，采用隔离法由牛顿第二定律研究．

本题难度：一般

4、选择题  双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动．研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化．若某双星系统中两星做圆周运动的周期为T，经过一段时间演化后，两星总质量变为原来的k倍，两星之间的距离变为原来的n倍，DC运动的周期为（　　）
A．