1、计算题  (14分)如图所示，光滑圆弧轨道最低点与光滑斜面在B点用一段光滑小圆弧平滑连接，可认为没有能量的损失，圆弧半径为R="0.5" m，斜面的倾角为450，现有一个可视为质点、质量为m="0.1" kg的小球从斜面上A点由静止释放，通过圆弧轨道最低点B时对轨道的压力为6 N。以B点为坐标原点建立坐标系如图所示(g="10" m/s2)。求：

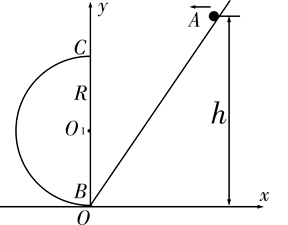
（1）小球最初自由释放位置A离最低点B的高度h；
（2）小球运动到C点时对轨道的压力的大小；
（3）小球从离开C点至第一次落回到斜面上，落点的坐标是多少?

参考答案：（1）小球最初自由释放位置A离最低点B的高度1.25 m；（2）小球运动到C点时对轨道的压力的大小为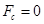；（3）小球从离开C点至第一次落回到斜面上，落点的坐标是（，）。

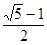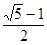本题解析：(1)由圆周运动向心力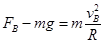
由动能定理得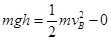
解得h="1.25" m。
(2)由动能定理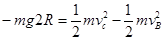 
圆周运动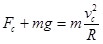 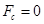,由作用力与反作用力的关系可得小球运动到C点时对轨道的压力FC′=-FC=0。
(3)设落点的坐标为（x,y），由平抛运动规律



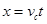
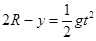
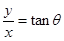
联立解得x=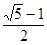，y=。
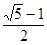则坐标为（，）。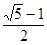
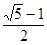考点：机械能守恒定律、向心力
点评：小球的运动过程可以分匀加速直线运动、机械能守恒运动及平抛运动，采用相应的规律求解即可。

本题难度：一般

2、填空题  在“验证机械能守恒定律”的实验中，已知打点计时器所用电源的频率为50Hz。查得当地的重力加速度为g＝9.80m/s2，某同学选择了一条理想的纸带，用刻度尺测量时各计数点对应刻度尺的读数如图所示。图中O点是打点计时器打出的第一个点，A、B、C、D分别是每隔一个点取出的计数点，它们到O点的距离如下图所示。重物质量m=1Kg,则重物由O点运动到B点时，求；

（1）重力势能减小量为        J
（2）动能的增加量为          J
（3）根据实验数据可以得出的结论是                
（4）产生误差的主要原因是                     

参考答案：（1）1.91    （3分） （2）1.88   （3分）
（3）在实验误差允许的范围内，动能的增加量等于重力势能的减少量（2分）
（4）物体在下落过程中克服摩擦阻力做功（2分）

本题解析：略

本题难度：一般

3、计算题  （14分）如图所示，固定的光滑圆弧面与质量为6 kg的小车C的上表面平滑相接，在圆弧面上有一个质量为2 kg的滑块A，在小车C的左端有一个质量为2 kg的滑块B，滑块A与B均可看做质点．现使滑块A从距小车的上表面高h＝1.25 m处由静止下滑，与B碰撞后瞬间粘合在一起共同运动，最终没有从小车C上滑出．已知滑块A、B与小车C的动摩擦因数均为μ＝0.5，小车C与水平地面的摩擦忽略不计，取g＝10 m/s2.求：

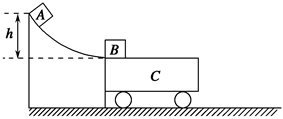
(1)滑块A与B碰撞后瞬间的共同速度的大小；
(2)小车C上表面的最短长度．

参考答案：(1)2.5 m/s (2)0.375 m

本题解析：(1)设滑块A滑到圆弧末端时的速度大小为v1，由机械能守恒定律有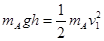：①
代入数据解得v1＝5 m/s.          ②
设A、B碰后瞬间的共同速度为v2，滑块A与B碰撞瞬间与车C无关，滑块A与B组成的系统动量守恒，
mAv1＝(mA＋mB)v2，             ③
代入数据解得v2＝2.5 m/s.           ④
(2)设小车C的最短长度为L，滑块A与B最终没有从小车C上滑出，三者最终速度相同设为v3，
根据动量守恒定律有：
(mA＋mB)v2＝(mA＋mB＋mC)v3          ⑤
根据能量守恒定律有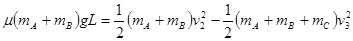： ⑥
联立⑤⑥式代入数据解得L＝0.375 m．        ⑦
考点：本题考查动量守恒、动能定理

本题难度：困难

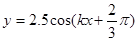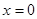4、计算题  （12分）在竖直平面内，一根光滑金属杆弯成如图所示形状，相应的曲线方程为（单位：），式中。将一光滑小环套在该金属杆上，并从处以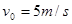的初速度沿杆向下运动，取重力加速度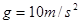。求

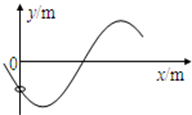
（1）当小环运动到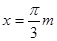时的速度大小；
（2）该小环最远能运动到的位置坐标多少？

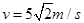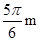参考答案：（1）    （2）（，0）

本题解析：（1）由曲线方程可知，环在x=0处的坐标是y1=-1.25m    1分)
在时，y2= -2.5m                  (1分)
选y=0处为零势能参考平面，根据机械能守恒有
，
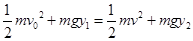解得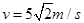            (4分)
（2）当环运动到最远处时，速度为零，根据机械能守恒有
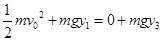 ，        (3分)
解得y3=0，            (1分)
即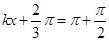，得     (1分)
该小环在x轴方向最远能运动到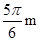（，0）处             (1分)
考点：本题考查机械能守恒定律。

本题难度：一般

5、其他  

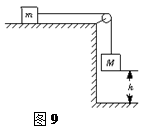
参考答案：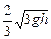

本题解析：以m和M组成的系统为研究对象，系统机械能守恒.则M下降h后速度为v，由机械能守恒定律得：系统减少的重力势能等于增加的动能，则
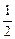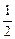Mgh=mv2+Mv2  ，
 
M=2m，
得v=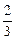

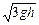
本题难度：简单