1、简答题 如图所示,斜面足够长,其倾角为α,质量为m的滑块,距挡板P为s0,以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面方向的重力分力,若滑块每次与挡板相碰均无机械能损失(即速度大小不变方向相反),求滑块在斜面上经过的总路程为多少?

参考答案:滑块在滑动过程中,要克服摩擦力做功,其机械能不断减少;又因为滑块所受摩擦力小于滑块沿斜面方向的重力分力,所以最终会停在斜面底端.
在整个过程中,受重力、摩擦力和斜面支持力作用,其中支持力不做功.设其经过和总路程为L,对全过程,由动能定理得:mgs0sinα-μmgLcosα=0-12mv20
解得:L=1μ(s0tanα+v202gcosα)
答:滑块在斜面上经过的总路程为1μ(s0tanα+v202gcosα).
本题解析:
本题难度:一般
2、计算题 过山车是游乐场中常见的设施,下图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k ="0.8)" ,相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数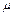 =0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
小题1:物块经过第一轨道最高点时的速度大小;
小题2:物块经过第二轨道最低点B时对轨道的压力大小;
小题3:物块能够通过几个圆轨道?
参考答案:
小题1:8m/s
小题2:77.5N
小题3:通过4个圆轨道
本题解析:
(1)设经第一个轨道最高点的速度为v,由机械能守恒有
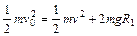
即有
(2)设物块经B点时的速度为vB,从A到B的过程由动能定理,

对物块经B点受力分析,由向心力公式有?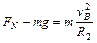
联立两式解得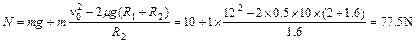
由牛顿第三定律可知,物块对轨道的压力大小为77.5N.
(3)设物块恰能通过第n个轨道,它通过第n个轨道的最高点时的速度为vn,有
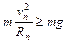
对物块从A到第n个轨道的最高点的全过程由动能定理得

又因为?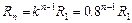
由以上三式可整理得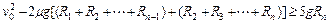
即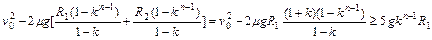
将v0=12m/s,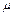 =0.5,R1=2m,k=0.8,g=10m/s2代入上式,整理得
=0.5,R1=2m,k=0.8,g=10m/s2代入上式,整理得 ,
,
即有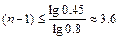 ,解得?
,解得?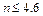
故物块共可以通过4个圆轨道.
本题难度:一般
3、计算题 如图所示,由细管道组成的竖直轨道,其圆形部分半径分别是R和R/2,质量为m的小球通过这段轨道时,在A处刚好对管壁无压力,在B点处对内轨道的压力为mg/2.
求:(1)小球分别通过A、B点的速度
(2)由A运动到B的过程中摩擦力对小球做的功.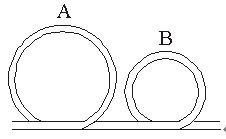
参考答案:(1)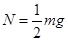 (2)
(2)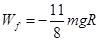
本题解析:(1)在A处,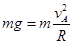 ?
? ?………………2分
?………………2分
在B处,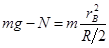
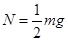
得 ?…………………………2分
?…………………………2分
由A到B,据动能定理

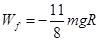 ?……………………………3分
?……………………………3分
本题难度:一般
4、填空题 如图所示,在竖直放置的平行金属板M、N之间有一带电微粒,自A点以初速度v0竖直向上进入场强为E的匀强电场后,正好垂直打在N板的B点,AC⊥BC,且AC=BC,则打在B点时微粒的速度是______,A、B点的电势差是______.
参考答案:设微粒从A运动到B的时间为t,AC=BC=d,则有
? 水平方向:v2t=d
? 竖直方向:v02t=d
得到,v=v0
研究竖直方向,得到
? 02-v20=-2gd
得,d=v202g
所以A、B点的电势差是U=Ed=Ev202g
故答案为:v0,Ev202g
本题解析:
本题难度:一般
5、简答题 如图所示,四个电阻阻值均为R,电键S闭合时,有一质量为m,带电量为q的小球静止于水平放置的平行板电容器的中点.现打开电键S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电量发生变化,碰后小球带有和该板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为d,不计电源内阻,求:
(1)电源电动势E多大?
(2)小球与极板碰撞后所带的电量为多少?
参考答案:(1)当S闭合时,电容器电压为U,则:U=E1.5R?R=23E?①
对带电小球受力分析得:qUd=mg?②
由①②式?解得:E=3mgd2q?③
(2)断开S,电容器电压为U′,则:U′=E2R?R=E2?④
对带电小球运动的全过程,根据动能定理得:q′U′-mgd2-qU′2=0?⑤
由③④⑤解得:q′=76q?⑥
答:
(1)电源电动势E是3mgd2q.
(2)小球与极板碰撞后所带的电量为76q.
本题解析:
本题难度:一般