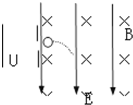
1、计算题  如图所示，在互相垂直的水平方向的匀强电场（E已知）和匀强磁场（B已知）中。有一固定的竖直绝缘杆，杆上套一个质量为m，电荷量为-q的小球，它们之间的动摩擦因数为μ，现由静止释放小球，试分析小球运动的加速度和速度的变化情况，并求出最大速度（mg>μqE）。

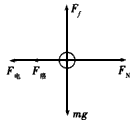
参考答案：解：当小球刚开始下落时，加速度最大，设为amax（如图）

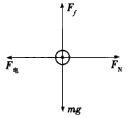
这时竖直方向有mg-Ff=mamax ①
在水平方向上有qE-FN=0 ②
又Ff=μFN ③
由①②③可得：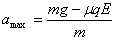
当下落有一定速度后

FN=F电+F洛=qE+qvB ④
mg-μFN=ma ⑤
由④⑤可得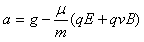： ⑥
由⑥式可得：随v增大，a减小，当a=0时v最大
故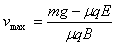

本题解析：

本题难度：困难

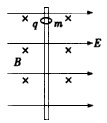
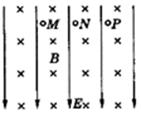
2、选择题  如图所示，匀强电场E的方向竖直向下，匀强磁场B的方向垂直纸面向里，让三个带有等量同种电荷的油滴M、N、P进入该区域中，M进入后能向左做匀速运动，N进入后能在竖直平面内做匀速圆周运动，P进入后能向右做匀速运动，不计空气阻力，则三个油滴的质量关系是(? )

A．mＭ＞mＮ＞mＰ　　
B．mＰ＞mＮ＞mＭ
C．mＮ＜mＭ＝mＰ　　
D．mＮ＞mＭ＝mＰ

参考答案：A

本题解析：若都带正电荷，则M向左做匀速直线运动，所以受力平衡，受到竖直向下的重力，竖直向下的洛伦兹力，和竖直向下的电场力，故不可能达到平衡，所以都带负电，所以M受到竖直向下的重力，竖直向上的电场力和洛伦兹力，即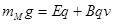，N做匀速圆周运动，所以电场力和重力抵消，故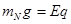,N向右做匀速直线运动，所以受到竖直向下的重力，竖直向下的洛伦兹力，竖直向上的电场力，即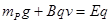，联立上述三式可得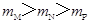，A正确，
点评：题关键分别对a、b、c三个液滴进行受力分析，然后得到液滴的电性，电场力和洛伦兹利的方向，最后根据共点力平衡条件得到液滴的重力的大小．

本题难度：一般

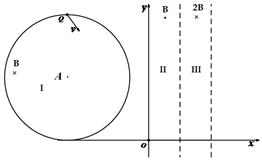
3、计算题  （18分）如图，在第二象限的圆形区域I存在匀强磁场，区域半径为R，磁感应强度为B，且垂直于Oxy平面向里;在第一象限的区域II和区域III内分别存在匀强磁场，磁场宽度相等，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面。质量为m、带电荷量q（q＞0）的粒子a于某时刻从圆形区域I最高点Q（Q和圆心A连线与y轴平行）进入区域I，其速度v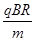＝?。已知a在离开圆形区域I后，从某点P进入区域II。该粒子a离开区域II时，速度方向与x轴正方向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b从P点进入区域II，其速度沿x轴正向，大小是粒子a的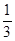。不计重力和两粒子之间的相互作用力。求：
（1）区域II的宽度；
（2）当a离开区域III时，a、b两粒子的y坐标之差.

参考答案：（1）?（2）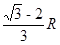

本题解析：（1）如图所示，a粒子进入区域I后，由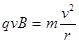
故a粒子在区域I做圆周运动的半径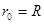?…………（1分）
其轨迹圆心为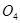,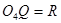且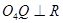
由几何知识得：
a粒子从某点D出射时，速度v沿x轴正方向. …………（2分）
a粒子从P点沿x轴正方向进入区域II后，由
得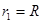?，可找到圆心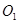?…………（1分）
作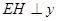轴，由图知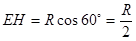：?，即磁场区域宽度?…………（2分）
(2)①对a粒子的运动进行分析：
进入区域Ⅲ后，由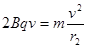，得……..（1分）
连接O1E并延长，取EO2=r2，则O2为a粒子在区域Ⅲ中的轨迹圆心延长HE交Ⅲ右边界于F，连接O2F
由已知条件易证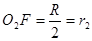，故F点是a粒子在区域Ⅲ中的出射点
且轨迹所对应的圆心角为60o
故a粒子在区域Ⅲ中运动的时间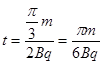…..（1分）
由图根据几何关系知：…..（1分）
②对b粒子的运动进行分析：
b粒子进入区域Ⅱ后，由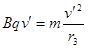，得：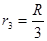
且其轨迹圆心O3位于y轴上
P点进入区域II，运动时间为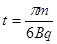?，故其轨迹所对应的圆心角为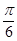…（1分）
由图根据几何知识：?…………（1分）
综上分析可知：
当a离开区域III时，a、b两粒子的y坐标之差为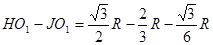
即坐标差为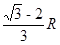? …………（2分）

本题难度：一般

4、选择题  如图所示，在第二象限内有水平向右的匀强电场，电场强度为E，在第一、第四象限内分别存在如图所示的匀强磁场，磁感应强度大小相等。有一个带电粒子以初速度v0垂直x轴，从x轴上的P点进入匀强电场，恰好与y轴成45°角射出电场，再经过一段时间又恰好垂直于x轴进入下面的磁场。已知OP之间的距离为d，则带电粒子

[? ]
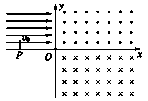
A．在电场中运动的时间为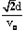
B．在磁场中做圆周运动的半径为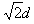
C．自进入磁场至第二次经过x轴所用时间为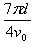
D．自进入电场至在磁场中第二次经过x轴的时间为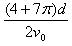

参考答案：D

本题解析：

本题难度：一般

5、选择题  放射源发出的α粒子（氦原子核）经电压为U的加速电场加速后进入正交的匀强电场E和匀强磁场B中，电场方向向下，磁场方向向内，如图所示，发现离子向下偏转，要使离子沿直线通过磁场，可以（　　）
A．增大电场强度E
B．增大磁感应强度B
C．增大加速电压U
D．减小加速电压U