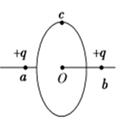
1、计算题  如图所示，a、b为两个固定的带正电q的点电荷，相距为L，通过其连线中点O作此线段的垂直平分面，在此平面上有一个以O为 圆心，半径为L的圆周，其上有一个质量为m，带电荷量为－q的点电荷c做匀速圆周运动，求c的速率。

参考答案：

本题解析：对c进行受力分析如图所示，由于c到O点距离R＝L，所以△abc是等边三角形。

a、b对c作用力F1＝F2＝，合力F合＝2F1cos 30°＝。
由牛顿第二定律得：F合＝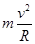
即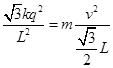解得：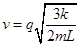

本题难度：一般

2、计算题  如图所示，竖直光滑直轨道OA高度为2R，连接半径为R的半圆形光滑环形管道ABC（B为最低点），其后连接圆弧环形粗糙管道CD，半径也为R．一个质量为m的小球从O点由静止释放，自由下落至A点进入环形轨道，从D点水平飞出，下落高度刚好为R时，垂直落在倾角为30°的斜面上P点，不计空气阻力，重力加速度为g．求：
（1）小球运动到B点时对轨道的压力大小；
（2）小球运动到D点时的速度大小；
（3）小球在环形轨道中运动时，摩擦力对小球做了多少功？

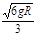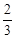参考答案：（1）N =7mg（2）（3）－mgR

本题解析：（1）O→B：3mgR=mυB2
B点：N– mg=m
N ˊ=" N" =7mg
（2）D→P：υy=gt? R=gt2
在P点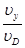：?=tan60°
υD=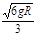
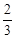（3）O→D：mgR+Wf =mυD2?Wf =－mgR
本题综合考查了曲线运动，根据牛顿第二定律可得小球在B点时对轨道的压力，要求小球在D点时的速度，可把运动过程逆过来球，现根据小球做平抛运动的规律求出平抛运动的初速度，即D点的速度从O到D整个过程中只有重力和摩擦力做功，可根据动能定理求得。

本题难度：简单

3、计算题  绳子系着装有水的小水桶，在竖直平面内作圆周运动，水的质量m=0.5Ｋg，绳长40cm，若不考虑桶的尺寸，求：?
①桶通过最高点时至少要有多大的速度水才不会流出？
②若水在最高点速度为V＝5m/s，水对桶的压力是多少？（g=10m/s2）

参考答案：①2m/s②26.25N

本题解析：（12分）要使水不流出，即所有的重力要充当向心力，即
mv2/r=mg……………………………..(3分)
v2="gr"
v="2m/s" ……………………………….（2分）
在最高点，速度为5m/s时
向心力 F=FN+mg=mv2/r…………………………(3分)
="31.25N"
故：FN＝31.25-mg=26.25N…………………….(2分)
根据牛顿第三定律可知水对水桶的压力为26.25N。（2分）

本题难度：简单

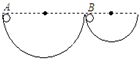
4、选择题  如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，两个质量不同的小球分别从与球心在同一水平高度的A、B两点由静止开始下滑，空气阻力不计，通过轨道最低点时（　　）
A．两小球的线速度大小相等
B．两小球的角速度相同
C．两小球的向心加速度相等
D．两小球对轨道的压力相同