1、选择题 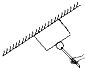 如图所示，在倾斜墙壁上用小轮压住一个木块处于静止状态，轮与木块间无摩擦；则木块
A.只受两个力
B.可以只受三个力
C.必然受到四个力
D.受三个或四个力均可能

参考答案：C

本题解析：分析：求解本题的关键是首先要将木块和小轮看做一个整体，然后再进行受力分析，根据平衡条件可知若无摩擦力则合力一定不能为零，再根据摩擦力产生的条件可知物块一定会受到弹力，故物块一定会受到四个力作用．
解答：将木块与小轮作为一个整体并对其受力分析如图所示：应有重力mg、推力F、弹力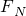和摩擦力f四个力，所以C正确ABD错误．
故选C．

点评：运动动力学问题首先要正确选取研究对象（对连接体问题一般采用“先整体后隔离”方法），然后按一定的程序进行受力分析，注意灵活运用假设法分析弹力和摩擦力的有无及方向．

本题难度：一般

2、选择题 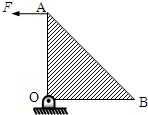 如图，一质量为M的不均匀三角板AOB，OA⊥OB且OA=OB=L，O点为水平固定转动轴，现用一水平拉力拉住A点，维持三角板处于OA竖直的静止状态，拉力大小为F，重力加速度为g，则三角板重心到AO的距离为
A.
B.
C.
D.

参考答案：A

本题解析：分析：以O点为支点，分析三角板AOB除O点以外受力情况，根据力矩平衡求解三角板重心到AO的距离．
解答：设三角板重心到AO的距离为x．三角板AOB除O点外，受到F和重力Mg，F的力臂为L，根据力矩平衡条件得
? FL=Mg?x
解得 x=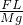
故选A
点评：本题是简单的力矩平衡问题，关键要正确找到力臂，由力矩平衡求解．

本题难度：一般

3、选择题  电磁打点计时器的打点周期决定于
A.交流电源电压的高低
B.交流电源的频率
C.永久磁铁的强弱
D.振针与复写纸间的距离

参考答案：B

本题解析：讲析：电磁打点计时器是利用电磁感应原理打点计时的一种仪器，当通过不高于10 V的低压交变电流时，在线圈和永久磁铁的作用下，振片便上下振动起来，位于振片一端的振针就跟着上下振动而打点，这时如果纸带运动，振针就在纸带上打出一系列点．
交流电源电压的高低和永久磁铁的强弱只影响振动片的受力大小，影响振片和振针的振动强弱，并不影响打点周期．振片实际上是在通入的交变电流产生的磁场力的作用下振动，振动周期(频率)等于交流电源的周期(频率)．所以只有选项B是正确的．
点评：本题考查了对打点计时器工作原理的理解，要对打点的频率有正确的认识，从而明确影响打点频率的因素是什么．

本题难度：简单

4、选择题  如图所示，Dl、D2规格相同的两个小灯泡，L是带有铁芯的电阻忽略不计的电感线圈，下列说法正确的是?

A.开关S接通瞬间，Dl、D2同时亮起来
B.开关S接通稳定后，Dl、D2亮度相同
C.开关S断开瞬间，Dl、D2同时熄灭
D.开关S断开的瞬间，D1立即熄灭．D2闪亮一下再逐渐熄灭

参考答案：AD

本题解析：分析：电感总是阻碍电流的变化．线圈中的电流增大时，产生自感电流的方向更原电流的方向相反，抑制增大；线圈中的电流减小时，产生自感电流的方向更原电流的方向相同，抑制减小，并与灯泡1构成电路回路．
解答：解：L是自感系数足够大的线圈，它的电阻可忽略不计，D1和D2是两个完全相同的小灯泡
A、S闭合瞬间，但由于线圈的电流增加，导致线圈中出现感应电动势从而阻碍电流的增加，所以两灯同时亮，当电流稳定时，由于电阻可忽略不计，所以以后D1熄灭，D2变亮．故A正确；
B、S闭合瞬间，但由于线圈的电流增加，导致线圈中出现感应电动势从而阻碍电流的增加，所以两灯同时亮，当电流稳定时，由于电阻可忽略不计，所以以后D1熄灭，D2变亮．故B错误；
C、S闭合断开，D2立即熄灭，但由于线圈的电流减小，导致线圈中出现感应电动势从而阻碍电流的减小，所以D1亮一下再慢慢熄灭，故C错误；
D、S闭合断开，D2立即熄灭，但由于线圈的电流减小，导致线圈中出现感应电动势从而阻碍电流的减小，所以D1亮一下再慢慢熄灭，故D正确；
故选：AD．
点评：线圈中电流变化时，线圈中产生感应电动势；线圈电流增加，相当于一个瞬间电源接入电路，线圈上端是电源正极．当电流减小时，相当于一个瞬间电源，线圈下端是电源正极．

本题难度：一般

5、选择题 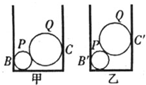 如图所示，两个光滑小球P、Q先后卡在宽度不同、内壁光滑的两个槽中．甲、乙两图中球P对槽底的压力分别为FA、F′A，对左侧壁B处和B′处的压力分别为FB、F′B，球Q对右侧壁C处和C′处的压力分别为FC、F′C，则
A.FA=F′A，FB=F′B，FC=F′C
B.FA=F′A，FB=-FC，F′B=-F′C
C.FA≠F′A，FB=-FC，F′B=F′C
D.FA=F′A，FB≠F′B，FC≠F′C

参考答案：BD

本题解析：分析：本题关键是灵活地选择研究对象，受力分析后根据平衡条件并结合合成法列式求解，得到各个弹力的一般表达式后再分析讨论．
解答：设两个球的球心连线与竖直方向的夹角为θ，先对Q球受力分析，受重力、P球的支持力和右壁的支持力，如图

根据平衡条件，有
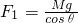? ①
F2=Mgtanθ? ②
根据牛顿第三定律，球对右侧容器壁的压力等于F2；
由②式，θ越大，球对右侧容器壁的压力越大，由于甲图中的θ大于乙图中的θ，故FC＞F′C；
再对两个球整体受力分析，受重力（M+m）g、容器底部的支持力N、容器左壁的支持力和容器右壁的支持力，如图

根据平衡条件，有
N=（M+m）g? ③
F3=F2? ④
由③式，并根据牛顿第三定律，球对容器底部的压力等于支持力N，与角度θ无关，故FA=F′A；
由④式，并根据牛顿第三定律，甲球对容器左侧的压力等于球对容器右壁的压力，即F2=F3=Mgtanθ，故FB=-FC；
由④式，并根据牛顿第三定律，乙球对左右两侧容器的 91ExAM.org压力也等大、反向，故F′B=-F′C；
由②④两式，球对容器左右壁压力都等于Mgtanθ，压力随θ的减小而减小，故FB＜F′B，FC＜F′C；
故选BD．
点评：连接体问题一般是指由两个或两个以上物体所构成的有某种关联的系统．研究此系统的受力或运动时，求解问题的关键是研究对象的选取和转换．一般若讨论的问题不涉及系统内部的作用力时，可以以整个系统为研究对象列方程求解---“整体法”；若涉及系统中各物体间的相互作用，则应以系统某一部分为研究对象列方程求解---“隔离法”．这样，便将物体间的内力转化为外力，从而体现其作用效果，使问题得以求解，在求解连接问题时，隔离法与整体法相互依存，交替使用，形成一个完整的统一体，分别列方程求解．

本题难度：一般