1、选择题 某人将一静止在地面上的物体提到空中某点A,此过程中重力做功W1,阻力做功W2,人对物体做功W3,以地面为参考平面,则在A点( )
A.物体的重力势能为?W1
B.物体的动能为W1+W2+W3
C.物体的动能为W3-W2-W1
D.物体的机械能为W3-W2
参考答案:A、物体重力势能的变化等于克服重力做的功,以地面为参考平面,即
△Ep=Ep末-0=-W1
?所以?Ep末=-W1,故A错误
?B、C、由动能定理知
△Ek=Ek末-0=W总=W1+W2+W3
?所以Ek末=W1+W2+W3,故B正确,C错误
?D、物体的机械能变化为除重力其它力做功之和,以地面为参考平面,即
△E=E末-0=W2+W3
? 所以E末=W2+W3,故D错误
故选B.
本题解析:
本题难度:一般
2、简答题 一运动员奋力将8 kg的铅球推出10 m远,铅球落地后将地面击出一坑,有经验的教练根据坑的深度认为铅球落地时的速度大约是12 m/s.若铅球出手时的高度为2 m,求推球过程中运动员对球做的功.
参考答案:416 J
本题解析:设球出手时的速度为v0,则运动员对球做的功W=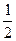 mv02
mv02
对球从以初速度v0抛出到落地的过程由动能定理得:mgh=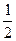 mv2-
mv2-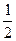 mv02,所以:
mv02,所以:
W=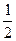 mv02=
mv02=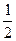 mv2-mgh=
mv2-mgh=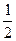 ×8×122 J-8×10×2 J="416" J.
×8×122 J-8×10×2 J="416" J.
本题难度:简单
3、计算题 如图所示,AB与CD为两个对称斜面,其上部足够长,下部分别与一个光滑的圆弧面的两端相切,圆弧的圆心角为120°,半径R为2.0m,一个物体在离弧底(E)高度h为3.0m处,以初速度4.0m/s沿斜面运动。若物体与两个斜面的动摩擦因数μ均为0. 02,则物体在两个斜面上(不包括圆弧部分)一共能走多少米?(取g=10m/s2)

参考答案:解:设物体在斜面上运动的总路程为s
则摩擦力所做的总功为- μmgscos60 °
末状态选为B点(或C点),此时物体的速度为0
对全过程应用动能定理得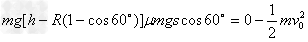
物体在斜面上通过的总路程为
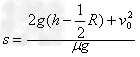
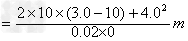
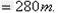
本题解析:
本题难度:一般
4、选择题 质量为m的物体在空中以0.9g(g为重力加速度)的加速度下落,在物体下落h高度的过程中,正确的是( )
A.重力势能减小了0.9mgh
B.动能增大了0.9mgh
C.动能增大了0.1mgh
D.机械能损失了0.9mgh
参考答案:A、重力做功等于重力势能的减少量,而W=mgh,故A错误
B、物体在空中以0.9g(g为重力加速度)的加速度下落,故合力F=0.9mg,由动能定理得,△Ek=Fh=0.9mgh,故B正确
C、由B分析得,C错误
D、机械能损失为0.1mgh,故D错误
故选B
本题解析:
本题难度:简单
5、计算题 质量为4t的卡车,由静止出发在水平公路上行驶100m后,速度增大到54km/h。若发动机的牵引力为5×103N不变,卡车克服阻力做了多少功?
参考答案:解:设牵引力为F
卡车克服阻力所做的功为Wf
根据动能定理有Fs-Wf=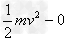
代入数据,解得Wf=5×104J
本题解析:
本题难度:一般
A quiet conscience sleeps in thunder. 心里坦然,打雷也照样入睡。