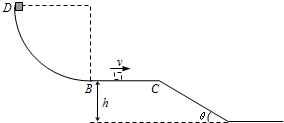
1、简答题  如图所示，半径R=0.9m的四分之一圆形光滑轨道竖直放置，圆弧最低点B与长为L=1m的水平面相切于B点，BC离地面高h=0.45m，C点与一倾角为θ=30°的光滑斜面连接，质量为m=1.0kg的小滑块从圆弧顶点D由静止释放，已知滑块与水平面间的动摩擦因数?=0.1，取g=10m/s2．试求：
（1）小滑块刚到达圆弧的B点时对圆弧的压力？
（2）小滑块到达C点时的速度？
（3）通过计算说明小滑块离开C点后是直接落到地面上还是直接落到斜面上？

参考答案：（1）设小滑块运动到B点的速度为VB，由机械能守恒定律有：
mgR=12mv2B
设轨道对滑块的支持力为N，由牛顿第二定律列方程得：
N-mg=mv2BR
联立二式得，N=30N
由牛顿第三定律得，小滑块刚到达圆弧的B点时对圆弧的压力为N′=30N
（2）设小滑块运动到C点的速度为VC，由动能定理有：
mgR-?mgL=12mVC2
解得小滑块在C点的速度：VC=4.0m/s
（3）小滑块平抛到地面的水平距离：S=VCt=VC

本题解析：

本题难度：一般

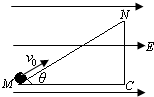
2、简答题  如图所示，把一个倾角为θ高度为h的绝缘斜面固定在匀强电场中，电场方向水平向右，电场强度大小为E，有一质量为m、带电荷量为+q的物体以初速度v0，从M点滑上斜面恰好能沿斜面匀速运动．求
（1）物体与斜面间的动摩擦因数
（2）物体从M到N过程中电势能的变化．

参考答案：（1）物体做匀速直线运动，由平衡条件得：
在垂直于斜面方向上：N=mgcosθ+qEsinθ，
在平衡与斜面方向上：f+mgsinθ=qEcosθ，
滑动摩擦力：f=μN，
解得：μ=qEcosθ-mgsinθmgcosθ+qEsinθ；
（2）物体从M到N过程中，电场力做正功：
W=qU=qEd=qEhcotθ，
物体电势能减少了qEhcotθ；
答：（1）物体与斜面间的动摩擦因数μ=qEcosθ-mgsinθmgcosθ+qEsinθ；（2）物体从M到N过程中电势能的变化为qEhcotθ．

本题解析：

本题难度：一般

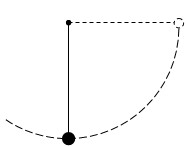
3、计算题  质量为m=2kg的小球用长为L=1.8米的细绳系住，另一端固定于O点，最初绳拉直且水平，由静止释放后，小球摆下来，求小球到过最低点时球的速度及绳的拉力多大？

参考答案：E初=E末
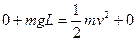?2分
?2分
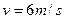?2分
F="60N?" ?2分

本题解析：略

本题难度：简单

4、选择题  质量为2kg的物体从静止开始，以8m/s2的加速度竖直向下匀加速运动了5m的距离．g取10m/s2，在这一过程中（　　）
A．物体的动能增加了160J
B．物体的重力势能增加了100J
C．物体的机械能减少了20J
D．合外力对物体做功80J

参考答案：A、根据动能定理有△E?k=mas=2×8×5J=80J，即动能增加了80J，所以A错误；
B、因物体向下运动，重力势能应减小，所以B错误；
C、根据牛顿第二定律有mg-f=ma得，f=4N，物体下落过程中阻力f做的功为W?f=-fs=-4×5J=-20J，再根据功能原理可知△E=W?f=-20J，即机械能减少了20J，所以C正确；
D、合外力对物体做功为W?总=mas=2×8×5J=80J，所以D正确．
故选CD．

本题解析：

本题难度：简单

5、计算题  如图，倾角为θ的光滑斜面上放有两个质量分别为m的小球A和B，两球之间用一根长为L的轻杆相连，下面的小球B离斜面底端的高度为h。两球从静止开始下滑，不计球与地面碰撞时的机械能损失，且地面光滑，求：

（1）两球在光滑水平面上运动时的速度大小；
（2）此过程中杆对A球所做的功；

参考答案：（1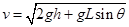）（2）

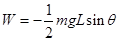
本题解析：（1）由于不计摩擦及碰撞时的机械能损失，因此两球组成的系统机械能守恒。两球在光滑水平面上运动时的速度大小相等，设为v，根据机械能守恒定律有：
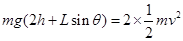? 4分
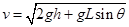解得：? 2分
（2）因两球在光滑水平面上运动时的速度v比B从h处自由滑下的速度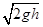大，
增加的动能就是杆对B做正功的结果。B增加的动能为：
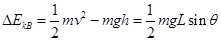? 4分
因系统的机械能守恒，所以杆对B球做的功与杆对A球做的功的数值应该相等，杆对B球做正功，对A做负功。
所以杆对A球做的功为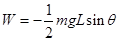：。 2分
点评：本题难度中等，明确整体的运动过程和做功过程是关键，巧妙应用能量守恒定律使计算过程变得简单

本题难度：一般