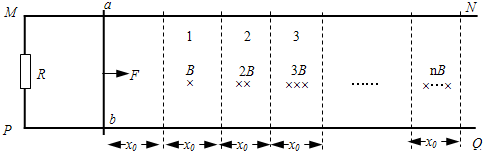
1、简答题  如图所示，两平行光滑的金属导轨MN、PQ固定在水平面上，相距为L，处于竖直向下的磁场中，整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成，从左向右依次排列，磁感应强度的大小分别为B、2B、3B…nB，两导轨左端MP间接入电阻R，一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上，与导轨电接触良好，不计导轨和金属棒的电阻．
（1）对导体棒ab施加水平向右的力，使其从图示位置开始运动并穿过n个磁场区，求导体棒穿越磁场区1的过程中通过电阻R的电量q；
（2）对导体棒ab施加水平向右的恒力F0，让它从磁场区1左侧边界处开始运动，当向右运动距离

参考答案：（1）电路中产生的感应电动势为：E=△Φ△t
通过电阻R的电量为：q=I△t=E△tR
导体棒通过I区过程：△Φ=BLx0
解得：q=BLx0R
故导体棒穿越磁场区1的过程中通过电阻R的电量：q=BLx0R．
（2）设导体棒运动时速度为v0，则产生的感应电流为：
I0=ER=BLv0R
导体棒受到的安培力与水平向右的恒力F0平衡，则
BI0L=F0
解得：v0=F0RB2L2
设棒通过磁场去I在△t时间内速度的变化为△v，对应的位移为△x，则
F0-BIL=m△v△t
△v=F0m△t-B2L2mRv△=F0m△t-B2L2mR△x
则∑△v=F0m∑△t-B2L2?mR∑△x
解得：t=B2L2x0F0R+mRB2L2
故棒通过磁场区1所用的时间t=B2L2x0F0R+mRB2L2．
（3）设进入I区时拉力为F1，速度v，则有：
F1x0=12mv2?
?F1-B2L2vR?=0
解得：F1=2B4L4x0mR2，v=2B2L2x0mR
进入i区的拉力：Fi=2i2B4L4x0?mR2．
导体棒以后通过每区域都以速度v做匀速运动，由功能关系有：
Q=F1x0+F2x0+…+Fnx0
解得：Q=2x20B4L4mR2(12+22+…n2)
故棒ab通过第i磁场区时的水平拉力的拉力：Fi=2i2B4L4x0?mR2，棒ab在穿过整个磁场区过程中回路产生的电热Q=2x20B4L4mR2(12+22+…n2)．

本题解析：

本题难度：一般

2、计算题  （12分）如图所示，有一初速可忽略的电子经电压U1＝500V加速后，进入两块水平放置、间距为d＝2cm、电压为U2＝10V的平行金属板A、B间。若电子从板正中央水平射入，且恰好能从B板的右端射出.求：

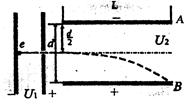
（1）金属板的长度L；
（2）电子离开电场的偏转的角度正切值tanθ;
（3）电子从B板右端射出电场时的动能Ek为多少电子伏特。

参考答案：

本题解析：（1）由动能定理和平抛知识可得：
，，，，，
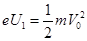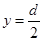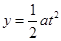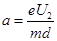（2）偏转的角度正切值：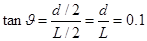
（3）由动能定理得：Ek=eU1+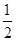eU2＝505eV

本题难度：一般

3、简答题  如图所示，质量M=0.8kg的小车静止在光滑的水平面上，左端紧靠竖直墙，在车上左端水平固定着一只弹簧，弹簧右端放一个质量m=0.2kg的滑块，弹簧为原长时，滑块位于C处（滑块可视为质点），车的上表面AC部分为光滑平面，CB部分为粗糙水平面，CB长L=1m，与滑块的摩擦因数μ=0.4，水平向左推动滑块，将弹簧压缩，然后再把滑块从静止释放，在压缩弹簧过程中推力做功2.5J，滑块释放后，将在车上往复运动，最终停在车上某处，设滑块与车的B端碰撞时机械能无损失，g=10m/s2．
求：（1）滑块释放后，第一次离开弹簧时的速度大小；
（2）滑块停在车上的位置离B端多远？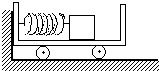

参考答案：（1）对滑块，由动能定理得：W=Ep=12mv2 -0，解得，滑块速度v0=5m/s；
（2）滑块与车组成的系统动量守恒，
由动量守恒定律得：mv0=（M+m）v，解得：车与滑块的共同速度v=1m/s，
车与滑块组成的系统，克服摩擦力产生的热量Q=μmgs=12mv2-12（M+m）v2；
解得，s=2.5m，滑块停在车上的位置离B端的距离d=s-2l=0.5m；
答：：（1）滑块释放后，第一次离开弹簧时的速度为5m/s；
（2）滑块停在车上的位置离B端为0.5m．

本题解析：

本题难度：一般

4、选择题  质量为1kg的物体，从0. 2 m高处从静止开始下落，空气阻力不计，物体落到地面时的动能为：(g取10N/kg)
A．0. 2 J
B．1 J
C．2 J
D．3 J

参考答案：C

本题解析：由功的公式可以求出合外力做的功，由动能定理可得，动能的改变等于合外力做的功；合外力做的功W合=mgh=2J，由动能定理可得，物体动能增加△EK=2J．

本题难度：简单

5、简答题  由相同材料的木板搭成的轨道如图，其中木板AB、BC、CD、DE、EF┅长均为L=1.5m，木板OA和其它木板与水平地面的夹角都为β=37°（sin37°=0.6，con37°=0.8），一个可看成质点的物体在木板OA上从图中的离地高度h=1.8m处由静止释放，物体与木板的动摩擦因数都为μ=0.2，在两木板交接处都用小曲面相连，使物体能顺利地经过它，既不损失动能，也不会脱离轨道．在以后的运动过程中，重力加速度取10m/s2，问：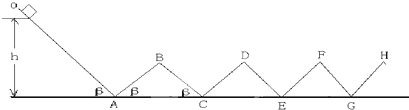
（1）物体能否静止在木板上？请说明理由．
（2）物体运动的总路程是多少？
（3）物体最终停在何处？并作出解释．

参考答案：（1）在斜面上物体重力沿斜面向下的分力为G1=mgsin37°=0.6mg，物体所受的摩擦力f=μmgcosθ=0.16mg．
由于f＜G1，故物体在木板上停不住．
（2）从物体开始运动到最终停下的过程中，总路程为s，由动能定理得，
mgh-μmgscos37°=0-0
代入数据解得s=11.25m．
（3）假设物体依次能到达B点、D点，由动能定理得，
mg（h-Lsin37°）-μmgcos37°×(hsin37°+L)=12mvB2-0，
解得vB＞0．
mg（h-Lsin37°）-μmgcos37°×(hsin37°+3L)=12mvD2-0，发现无解．
说明物体能通过B点，到不了D点，最终停在C点处．
答：（1）物体不能静止在木板上．
（2）物体运动的总路程为11.25m．
（3）物体最终停止在C处．

本题解析：

本题难度：一般