微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 如图所示,三个可视为质点的物块A,B,C,在水平面上排成一条直线,且彼此间隔一定距离。已知mA=mB=10 kg,mC=20 kg,C的左侧水平面光滑,C的右侧水平面粗糙,A,B与粗糙水平面间的动摩擦因数μA=μB=0.4,C与粗糙水平面间动摩擦因数μC=0.2,A具有20 J的初动能向右运动,与静止的B发生碰撞后粘在一起,又与静止的C发生碰撞,最后A,B,C粘成一个整体,求:(取g=10 m/s2)
(1)在第二次碰撞中损失的机械能有多少?
(2)这个整体在粗糙的水平面上滑行的距离是多少?

参考答案:解:(1)由于A的初动能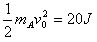
得A的初速度v0=2 m/s
A,B发生完全非弹性碰撞,根据动量守恒定律
mAv0=(mA+mB)v1,得v1=1 m/s
A,B与C发生完全非弹性碰撞,根据动量守恒定律
(mA+mB)v1=(mA+mB+mC)v2,得v2=0.5 m/s
在第二次碰撞中损失的机械能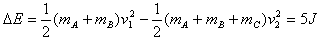
(2)A,B,C整体在粗糙水平面上所受的摩擦力f=fA+fB+fC=μAmAg+μBmBg+μCmCg=120 N
根据动能定理
解得
本题解析:
本题难度:困难
2、计算题 质量分别为m1、m2的A、B两小球在同一条直线上发生弹性正碰,它们在碰撞前后的s-t图象如图所示,已知小球A的质量m1=1 kg,则小球B的质量m2为多少?
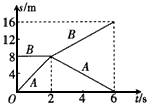
参考答案:解:从s-t图象上可看出,碰前小球B的速度为0
小球A的速度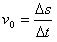 =4 m/s
=4 m/s
碰后,小球A的速度 m/s=-2 m/s
m/s=-2 m/s
小球B的速度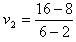 m/s=2 m/s
m/s=2 m/s
由动量守恒定律得:m1v0=m1v1+m2v2
解得:m2=3 kg
本题解析:
本题难度:一般
3、选择题 如图所示,在水平面上安装半径为R的半圆竖直挡板,质量为2m的b球静止在挡板中央;质量m的小球从斜面上高为R/2处静止释放,到达水平面恰能贴着挡板内侧运动,并与b球发生正碰,碰后a球静止。不计小球体积,不计所有摩擦。则
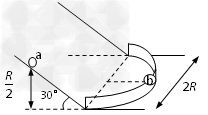
[? ]
A.碰前a球受到挡板的压力为0.5mg
B.碰前a球受到挡板的压力为mg
C.碰后b球恰好运动到对面轨道的R/2高度
D.碰后b球只能运动到对面轨道的R/8高度
参考答案:BD
本题解析:
本题难度:一般
4、简答题 如图16-4-13所示,质量均为m的A、B两个弹性小球,用长为2l的不可伸长的轻绳连接,现把A、B两球置于距地面高H处(H足够大),间距为l,当A球自由下落的同时,将B球以速度v0指向A球水平抛出.求:

图16-4-13
(1)两球从开始运动到相碰,A球下落的高度;
(2)A、B两球碰撞(碰撞时无机械能损失)后,各自速度的水平分量;
(3)轻绳拉直过程中,B球受到绳子拉力的冲量大小.
参考答案:(1) h= .③
.③
(2)  =v0,
=v0, =0.
=0.
(3) m .
.
本题解析:(1)设A球下落的高度为h,
l=v0t,①
h=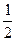 gt2②
gt2②
联立①②得h= .③
.③
(2)由水平方向动量守恒得
mv0=mvAx′+mvBx′④
由机械能守恒得
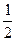 m(v02+
m(v02+ )+
)+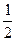 m
m =
=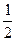 m(vA′2+
m(vA′2+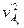 )+
)+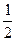 m(
m(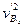 +
+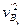 ) ⑤
) ⑤
式中 ,
, .
.
联立④⑤得 =v0,
=v0, =0.
=0.
(3)由水平方向动量守恒得mv0=2mvBx″,
l=mvBx″=m .
.
本题难度:简单
5、选择题 如图所示,质量为M的长木板静止在光滑的水平地面上,在木板的右端有一质量为m的小铜块,现给铜块一个水平向左的初速度v0,铜块向左滑行并与固定在木板左端的长度为L的轻弹簧相碰,碰后返回且恰好停在长木板右端。根据以上条件可以求出的物理量是?
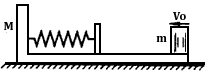
[? ]
A.轻弹簧与铜块相碰过程中所具有的最大弹性势能
B.整个过程中转化为内能的机械能
C.长木板速度的最大值
D.铜块与长木板之间的动摩擦因数
参考答案:A
本题解析:
本题难度:一般