1、填空题  如图所示，LMN是竖直平面内固定的光滑绝缘轨道，MN水平且足够长，LM下端与MN相切．在虚线OP的左侧，有一竖直向下的匀强电场E1，在虚线OP的右侧，有一水平向右的匀强电场E2和垂直纸面向里的匀强磁场B．C、D是质量均为m的小物块（可视为质点），其中C所带的电荷量为+q，D不带电．现将物块D静止放置在水平轨道的MO段，将物块C从LM上某一位置由静止释放，物块C沿轨道下滑进入水平轨道，速度为v，然后与D相碰，粘合在一起继续向右运动．求：

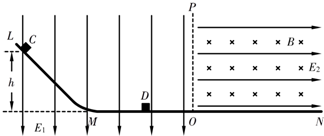
（1）物块C从LM上释放时距水平轨道的高度h；
（2）物块C与D碰后瞬间的共同速度v共；
（3）物块C与D离开水平轨道时与OP的距离x．

参考答案：（1）物块C下滑过程中，由动能定理得：
(mg+qE1)h=12mv2-0，
解得：h=mv22(mg+qE1)；
（2）物块C、D碰撞过程动量守恒，以C、D组成的系统为研究对象，以C的初速度方向为正方向，
由动量守恒定律得：mv=（m+m）v共，解得：v共=v2；
（3）C与D刚要离开水平轨道时对轨道的压力为零，
设此时它们的速度为v′，在竖直方向上，qv"B=2mg…①
CD一起向右运动过程中，由动能定理得：qE2x=12×2mv′2-12×2mv2共…②
由①②解得：x=m2qE2(4mg2q2B2-v24)；
答：（1）物块C从LM上释放时距水平轨道的高度h=mv22(mg+qE1)；
（2）物块C与D碰后瞬间的共同速度v共=v2；
（3）物块C与D离开水平轨道时与OP的距离x=m2qE2(4mg2q2B2-v24)．

本题解析：

本题难度：一般

2、简答题  如图所示，光滑水平面上有一辆质量为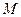=1kg的小车，小车的上表面有一个质量为=0.9kg的滑块，在滑块与小车的挡板间用轻弹簧相连接，滑块与小车上表面间的动摩擦因数为μ=0.2，整个系统一起以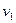=10m/s的速度向右做匀速直线运动，此时弹簧长度恰好为原长．现在用一质量为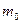=0.1kg的子弹，以=50m./s的速度向左射入滑块且不穿出，所用时间极短，当弹簧压缩到最短时，弹簧被锁定，测得此时弹簧的压缩量为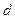=0.50m， g =10m/s2．求：

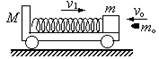
（1）子弹射入滑块后的瞬间，子弹与滑块共同速度的大小和方向；
（2）弹簧压缩到最短时，小车的速度和弹簧的弹性势能的大小．

参考答案：
（1）v2= 4m/s，方向水平向右； ?（2）8 J

本题解析：
⑴　子弹射入滑块后的共同速度大为v2，设向右为正方向，对子弹与滑块组成的系统应用动量守恒定律得
mv1—mv0= （m+m0） v2　　　?（4分）
v2= 4m/s，方向水平向右；?（2分）
⑵子弹，滑块与小车，三者的共同速度为v3，当三者达到共同速度时弹簧压缩量最大，弹性势能最大．由动量守恒定律得
Ｍv1+（m+m0）v2 = （M+m+m0）v3　?（3分）
v3=7m/s，方向水平向右． ?（2分）
设最大弹性势能为防Ｅpmax对三个物体组成的系统应用能量守恒定律
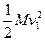＋（m+m0）v22 ="?" EPmax + （M+m+m0） v32+μ（m+m0）gd?（3分）
EPmax=" 8" J?（2分）

本题难度：简单

3、计算题  如图所示，甲车质量m1=20kg，车上有质量M=50kg的人，甲车（连同车上的人）从足够长的斜坡上高h=0.45m由静止滑下，到水平面上后继续向前滑动。此时质量m2=50kg的乙车正以v0=1.8m/s的速度迎面滑来，为了避免两车相撞，当两车相距适当距离时，人从甲车跳到乙车上，求人跳出甲车的水平速度（相对地面）应在什么范围以内？不计地面和斜坡的摩擦，取g=10m/s2。?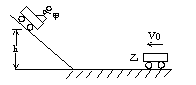

参考答案：3.8 m/s≤v≤4.8 m/s

本题解析：甲车（包括人）滑下斜坡后速度：v甲="2gh=3" m/s,在人跳离甲车和人跳上乙车过程中各自动量守恒，设人跳离甲车和跳上乙车后，两车速度分别为v甲′和v乙′，则：
（M+m1)v甲=Mv+m1v甲′?①?
Mv-m2v0=(M+m2)v乙′?②?
恰不发生相撞的条件为：v甲′=±v乙′?③?
从①得：v甲′=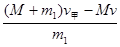
从②得：v乙′=
当v甲′=v乙′时，有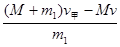=时，得v="3.8" m/s?
当v甲′=－v乙′时，有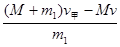=－时，得v="4.8" m/s?
所以，人跳离甲车的速度（对地）应满足3.8 m/s≤v≤4.8 m/s。
根据动量守恒求得甲、乙碰后的速度，然后再判断两个速度的关系，从而求出速度范围。

本题难度：一般

4、选择题  鱼雷快艇的总质量为M，以速度υ前进，现沿快艇前进方向发射一颗质量为m的鱼雷后，快艇速度减为原来的

参考答案：根据动量守恒定律有：Mv=（M-m）13v+mv′．
解得v′=2M+m3mv．
故A正确，B、C、D错误．
故选A．

本题解析：

本题难度：简单

5、计算题  如图所示，质量为m=3.0kg的小车在光滑水平轨道上以v1=2.0m/s速度向右运动．一股水流以v2=2.4m/s的水平速度自右向左射向小车后壁。已知水流流量为Q=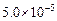m3/s，射到车壁的水全部流入车厢内．那么，经多长时间可使小车静止？（水的密度为ρ=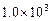kg/m3），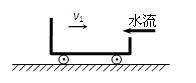

参考答案：由题意知，小车质量m="3.0kg" ，速度v1=2.0m/s；水流速度v2=2.4m/s，水流流量Q=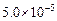m3/s，水的密度ρ=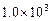kg/m3.
设经t时间，流人车内的水的质量为M，此时车开始反向运动，车和水流在水平方向没有外力，动量守恒，所以有?mv1- Mv2="0?" ①
又因为?M=ρV ?②
V=Qt? ③
由以上各式带入数据解得?t="50s?" ④

本题解析：略

本题难度：一般