1、计算题   如图所示，质量m="0.1kg" 的小球在细绳的拉力作用下在竖直面内做半径为r="0.2m" 的圆周运动，已知小球在最高点的速率为v1=2m/s，g 取10m/s2．求：

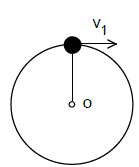
（1）小球在最高点时所受拉力；
（2）小球在最低点时的速率．

参考答案：（1）?（2）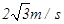

本题解析：（1）受力分析：? (2分)

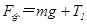? (1分)
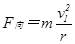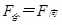? (1分)
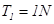?（1分）
?（1分）
（2）由高到低到对小球动能定理 ：
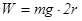?（2分）
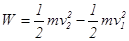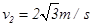?（1分）
?（1分）

本题难度：一般

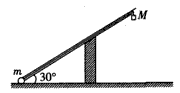
2、计算题  如图所示，长为L、内壁光滑的直管与水平地面成30°角固定放置，将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M=km的小物块相连，小物块悬挂于管口，现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变。(重力加速度为g)
(1)求小物块下落过程中的加速度大小；
(2)求小球从管口抛出时的速度大小；
(3)试证明小球平抛运动的水平位移总小于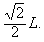

参考答案：解：(1)设细线中的张力为T，根据牛顿第二定律，有：
Mg-T=Ma，T-mgsin30°=ma
且M=km
解得：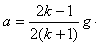
(2)设M落地时的速度大小为v，m射出管口时速度大小为v0，M 落地后m的加速度为a0。根据牛顿第二定律有：-mgsin30°=ma0
匀变速直线运动，有：v2=2aLsin30°，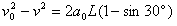
解得：
(3)平抛运动x=v0t，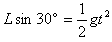
解得
则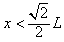，得证

本题解析：

本题难度：困难

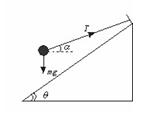
3、计算题  一个质量为0．2 kg的小球用细线吊在倾角θ=53°的斜面顶端，如图，斜面静止时，球紧靠在斜面上，绳与斜面平行，不计摩擦，当斜面以10 m/s2的加速度向右做加速运动时，求绳的拉力及斜面对小球的弹力．（计算时）?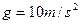

参考答案：2．83 N? N =0

本题解析：当加速度a较小时，小球与斜面体一起运动，此时小球受重力、绳拉力和斜面的支持力作用，绳平行于斜面，当加速度a足够大时，小球将“飞离”斜面，此时小球受重力和绳的拉力作用，绳与水平方向的夹角未知，题目中要求a="10" m/s2时绳的拉力及斜面的支持力，必须先求出小球离开斜面的临界加速度a0．（此时，小球所受斜面支持力恰好为零）
由mgcotθ=ma0
所以a0=gcotθ=7．5 m/s2
因为a="10" m/s2＞a0
所以小球离开斜面N=0，小球受力情况如图2-7，则Tcosα=ma,
Tsinα=mg
所以T=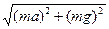=2．83 N,? N =0．

本题难度：一般

4、简答题  在光滑水平面上有一质量m=1.0kg的小球，静止在O点．以O点为原点，在该水平面内建立直角坐标系Oxy．现突然加一沿X轴正方向、大小F=2.0N的恒力，使小球开始运动．经过1.0s，所加恒力突然变为沿y轴正方向，大小仍为F=2.0N．再经过1.0s，所加恒力变为F"，使小球在恒力F"在作用下经1.0s速度变为零．求此恒力F"方向及速度变为零时小球的位置．

参考答案：第1秒小球做匀加速直线运动根据牛顿第二定律和运动学公式得：
ax=Fm=21m/s2=2m/s2
x方向的速度：vx=axt=2×1=2m/s
x方向位移：x1=12axt2=1m
第2秒内小球做类平抛运动：
ay=Fm=21m/s2=2m/s2
vy=ayt=2×1=2m/s
x方向位移：x2=vxt=2×1=2m
y方向位移：y2=12ayt2=1m
第2秒末小球速度方向与x轴正方向的夹角
tanθ=vyvx=1，
即速度方向与x轴正方向成45°角，所以F"方向与速度方向相反，与x轴正方向成135°角
第3秒小球必定做匀减速直线运动：
x3=12vxt′=1m
y3=12vyt′=1m
小球位置：x=x1+x2+x3=4m
y=y2+y3=2m
即：（4m，2m）
答：所以F"方向与速度方向相反，与x轴正方向成135°角；小球位置坐标（4m，2m）．

本题解析：

本题难度：一般

5、简答题  如图（a）所示，平行金属导轨MN、PQ光滑且足够长，固定在同一水平面上，两导轨间距L=0.25m，电阻R=0.5Ω，导轨上停放一质量m=0.1kg、电阻r=0.1Ω的金属杆，导轨电阻可忽略不计，整个装置处于磁感强度B=0.4T的匀强磁场中，磁场方向竖直向下，现用一外力F沿水平方向拉杆，使其由静止开始运动，理想电压表的示数U随时间t变化的关系如图（b）所示．试分析与求：

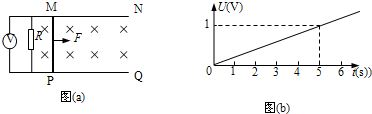
（1）分析证明金属杆做匀加速直线运动；
（2）求金属杆运动的加速度；
（3）写出外力F随时间变化的表达式；
（4）求第2.5s末外力F的瞬时功率．

参考答案：
（1）U=ε?RR+r=BLvRR+r，
U∝v，因U随时间均匀变化，
故v也随时间均匀变化，金属杆做匀加速直线运动．?
（2）k=△U△t=△v△t?BLRR+r=a?BLRR+r
解得：a=k(R+r)BLR=0.2×(0.5+0.1)0.4×0.25×0.5=2.4（m/s2）?
（3）F=F安+ma=BIL+ma=B2L2atR+r+ma=0.04t+0.24
（4）P=Fv=（0.04t+0.24）at=2.04W?
答：（1）因U随时间均匀变化，故v也随时间均匀变化，金属杆做匀加速直线运动；
（2）则金属杆运动的加速度2.4m/s2；
（3）外力F随时间变化的表达式为F=0.04t+0.24；
（4）则第2.5s末外力F的瞬时功率2.04W．

本题解析：

本题难度：一般