1、计算题  如图所示，一倾角为θ=37o的绝缘斜面高度为h=3.6m，底端有一固定挡板，整个斜面置于匀强电场中，场强大小为E=1×106N/C，方向水平向右。现有一质量为m=1.1kg，电荷量为q=－1×10－6C的小物体，沿斜面顶端从静止开始下滑，小物体与斜面间的动摩擦因数为?=0.5，且小物体与挡板碰撞时不损失机械能(g=10m/s2,sin37o=0.6，cos37o=0.8）求：

（1）小物体第一次与挡板碰撞前瞬间速度v的大小；
（2）小物体从静止开始下滑到最后停止运动通过的总路程s．

参考答案：（1）（2）

本题解析：（1）对滑块受力分析，由力的平行四边形定则可求出滑动摩擦力的大小，再根据动能定理列出表达式，从而求出第一次碰撞时滑块的速度大小；
（2）由滑块与斜面摩擦产生热量，从而可求出第二次碰撞后回到水平面时比原来相比向右移动的距离；由于电场力大于重力沿斜面分力与滑动摩擦力之和，则滑块最终停在C处，从而由动能定理可求出总路程．
对物块进行受力分析，如图所示?

解法一：


根据牛顿第二定律得
?
联立代入数据得
?
又??
由?
则 ?
解法二：在运动过程中重力、静电力、摩擦力做功，
根据动能定理得?
?

?
联立代入数据得
?
（2）整个过程中重力、静电力、摩擦力做功，
根据动能定理得

代入数据得
?
点评：考查动能定理、力的平行四边形定则，并让学生知道动能定理过程选取的重要性，同时搞清电场力、重力做功与路径无关，摩擦力做功与路径有关．

本题难度：一般

2、简答题  

（1）求此区域内电场强度的大小和方向.
（2）若某时刻微粒在场中运动到P点时，速度与水平方向的夹角为60°，且已知P点与水平地面间的距离等于其做圆周运动的半径.求该微粒运动到最高点时与水平地面间的距离.
（3）当带电微粒运动至最高点时，将电场强度的大小变为原来的1/2（不计电场变化对原磁场的影响），且带电微粒能落至地面，求带电微粒落至地面时的速度大小.

参考答案：（1）mg/q?方向竖直向上（2）（3）

本题解析：（1）由于带电微粒可以在电场、磁场和重力场共存的区域内沿竖直平面做匀速圆周运动，表明带电微粒所受的电场力和重力大小相等、方向相反。

因此电场强度的方向竖直向上? ………………………… 2分
设电场强度为E，则有mg=qE，即E=mg/q?………………………… 3分
（2）设带电微粒做匀速圆周运动的轨道半径为R，根据牛顿第二定律和洛仑兹力公式有?qvB=mv2/R，解得R=?…………………………4分
依题意可画出带电微粒做匀速圆周运动的轨迹，由如图所示的几何关系可知，
该微粒运动最高点与水平地面间的距离
hm=5R/2=?…………………………? 2分
（3）将电场强度的大小变为原来的1/2，则电场力变为原来的1/2，即F电=mg/2
带电微粒运动过程中，洛仑兹力不做功，所以在它从最高点运动至地面的过程中，只有重力和电场力做功。设带电微粒落地时的速度大小为vt，根据动能定理有
mghm-F电hm=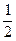mvt2-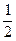mv2? …………………………3分
解得：? ………………………… 2分

本题难度：一般

3、简答题  光滑绝缘水平面上有一个带电质点正以速度v向右匀速运动．如果加一个水平方向的匀强电场，经过一段时间后，该质点的速度与初始速度等大反向；如果不加电场，而加一竖直向下的匀强磁场，经过相同的时间，该质点的速度也与初始速度等大反向，求匀强电场的电场强度E和匀强磁场的磁感应强度B的比值

参考答案：带电质点（设电量为q，质量为m）所受重力与水平面的支持力平衡，只加电场时，根据牛顿第二定律，有：qE=ma
根据速度时间关系公式，有：-v=v-at
解得：E=2mvqt
只加磁场时，根据牛顿第二定律，有：qvB=mv2r
则周期：T=2πrv=2πmqB
质点经t时间速度等大反向，则：
t=(2n+1)?T2（n=0，1，2，…）
解得：B=(2n+1)πmqt（n=0，1，2，…）
所以EB=2v(2n+1)π（n=0，1，2，…）
答：匀强电场的电场强度E和匀强磁场的磁感应强度B的比值EB=2v(2n+1)π（n=0，1，2，…）．

本题解析：

本题难度：一般

4、选择题  如图所示，实线表示在竖直平面内的匀强电场的电场线，电场线与水平方向的夹角为α，水平方向的匀强磁场与电场线正交，有一带电液滴沿斜向上的虚线l做直线运动．l与水平方向的夹角为β，且α＞β则下列说法中正确的是（　　）
A．液滴一定做匀速直线运动
B．液滴一定带负电
C．电场线方向一定斜向下
D．液滴也有可能做匀变速直线运动