1、计算题  如下图所示，水平轨道AB与位于竖直面内半径为R="0.90" m的半圆形光滑轨道BCD相连，半圆形轨道的BD连线与AB垂直。质量为m=1.0kg可看作质点的小滑块在恒定外力F=17.5N作用下从水平轨道上的A点由静止开始向右运动，物体与水平地面间的动摩擦因数μ=0.5。到达水平轨道的末端B点时撤去外力，已知AB间的距离为x=1.8m，滑块进入圆形轨道后从D点抛出，求滑块经过圆形轨道的B点和D点时对轨道的压力是多大？（g取10m/s2）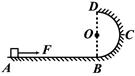

参考答案：60N? 0

本题解析：由动能定理，得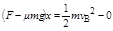?（2分）
在B点有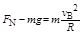?（2分）
联系解得? FN="60N"
由牛顿第三定律知，滑块在B点对轨道的压力大小为60N （1分）
滑块由B点到D点过程由动能定理，得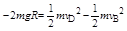?（2分）
在D点有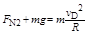?（2分）
联立解得? FN2="0?"
由牛顿第三定律知滑块在D点对轨道的压力大小为0 （1分）

本题难度：一般

2、计算题  小球自h=2m的高度由静止释放，与地面碰撞后反弹的高度为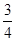h.设碰撞时没有动能的损失，且小球在运动过程中受到的空气阻力大小不变，且以后每碰撞地面一次弹起的高度为碰前的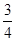倍 .求：
（1）小球受到的空气阻力是重力的多少倍？
（2）小球运动的总路程.

参考答案：（1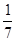）? mg（2）14 m

本题解析：设小球质量为m，所受阻力大小为F
（1）小球从h处释放时速度为零，与地面碰撞反弹到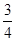 h时，速度也为零，
由动能定理得mg(h-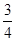? h)-F（h+ 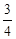?h）=0?（3分）
解得F= 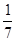?mg? (3分)
（2）设小球运动的总路程为s，且最后小球静止在地面上，由动能定理得：
mgh-Fs=0?（3分）
s=?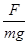?h=7×2 m="14" m? (3分)

本题难度：一般

3、简答题  一宠物毛毛狗“乐乐”在玩耍时不慎从离地h1=19.5m高层阳台无初速度竖直掉下，当时刚好是无风天气，设它的质量m=2kg，在“乐乐”开始掉下的同时，几乎在同一时刻刚好被地面上的一位保安发现并奔跑到达楼下，奔跑过程用时2.5s，恰好在距地面高度为h2=1.5m处接住“乐乐”，“乐乐”缓冲到地面时速度恰好为零，设“乐乐”下落过程中空气阻力为其重力的0.6倍，缓冲过程中空气阻力为其重力的0.2倍，重力加速度g=10m/s2．求：
（1）为了营救“乐乐”允许保安最长的反应时间；
（2）在缓冲过程中保安对“乐乐”做的功．

参考答案：（1）对“乐乐”用牛顿第二定律mg-0.6mg=ma1求得：a1=4m/s2?
“乐乐”下落过程：h1-h2=12a1t2
求得：t=3s?
允许保安最长反应时间：t=（3-2.5）s=0.5s?
（2）“乐乐”下落18m时的速度υ1=a1t=12m/s?
缓冲过程中，对“乐乐”由动能定理得：W+mgh2-0.2mgh2=0-12mυ12
解得：W=-168J?
答：（1）为了营救“乐乐”允许保安最长的反应时间为0.5s；（2）在缓冲过程中保安对“乐乐”做的功-168J．

本题解析：

本题难度：一般

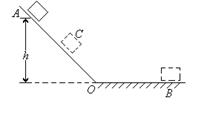
4、选择题  如图所示，物体从A处开始沿光滑斜面AO下滑，又在粗糙水平面上滑动，最终停在B处。已知A距水平面OB的高度为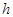，物体的质量为m，现将物体m从B点沿原路送回至AO的中点C处，需外力做的功至少应为　

A．mgh/2
B．mgh
C．2 mgh
D．3mgh/2

参考答案：D

本题解析：由动能定理mgh-Wf=0，W-mgh/2- Wf=0，联立解得W=3mgh/2，选项D正确。

本题难度：一般

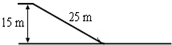
5、简答题  斜雪道的长为25m，顶端高为15m，下端经过一小段圆弧过渡后与很长的水平雪道相接，如图所示．一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出，在落到倾斜雪道上时，运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起．除缓冲外运动员可视为质点，过渡轨道光滑，其长度可忽略．设滑雪板与雪道的动摩擦因数μ=0.2，求
（1）运动员落到倾斜雪道上时速度大小
（2）运动员在水平雪道上滑行的距离（取g=10m/s2）

参考答案：（1）设平抛运动的水平分位移为x，竖直分位移为y，根据几何关系，有
y=x?tanθ=34x
运动员飞出后做平抛运动
x=v0t
y=12gt2
联立三式，得飞行时间：t=1.2 s
落点的x坐标：x1=v0t=9.6 m
落点离斜面顶端的距离：s1=12gt2sinθ=12m
落点距地面的高度：h1=（L-s1）sinθ=7.8m
接触斜面前的x分速度：vx=8m/s
y分速度：vy=gt=12m/s
沿斜面的速度大小为：vB=vxcosθ+vy sinθ=13.6m/s
即运动员落到倾斜雪道上时速度大小为13.6m/s．
（2）设运动员在水平雪道上运动的距离为s2，由功能关系得：
mgh1+12mvB2=μmgcosθ（l-s1）+μmgs2
解得：s2=74.8 m
即运动员在水平雪道上滑行的距离为74.8m．

本题解析：

本题难度：一般