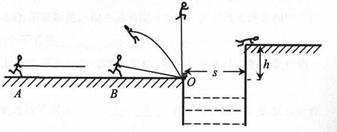
1、简答题  如图所示，一位质量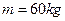参加“挑战极限”的业余选手，要越过一宽度为的水沟，跃上高为的平台．采用的方法是：人手握一根长的轻质弹性杆一端，从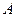点由静止开始匀加速助跑，至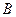点时，杆另一端抵在O点的阻挡物上，接着杆发生形变、同时脚蹬地，人被弹起，到达最高点时杆处于竖直状态，人的重心在杆的顶端，此刻人放开杆水平飞出，最终趴落到平台上，运动过程中空气阻力可忽略不计．
（1）设人到达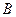点时速度，人匀加速运动的加速度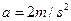，求助跑距离SAB；
（2）人要到达平台，在最高点飞出时刻速度至少多大？(取g=10m／s2)
（3）设人跑动过程中重心离地高度，在(1)、(2)问的条件下，在B点蹬地弹起瞬间，人至少再做多少功？

参考答案：（1）?（2）（3）

本题解析：（1）因为人从A到B做匀加速运动，


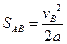
（2）人到达最高点时放开杆水平飞出，作平抛运动，最终趴落到平台上

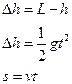
由以上各式得：速度至少
（3）人在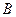点蹬地弹起瞬间，人做功为人的杆组成的系统机械能增量

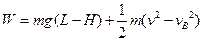
由以上式得：人至少做功为

本题难度：一般

2、简答题  如图所示，质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上，从A点随传送带运动到水平部分的最右端B点，经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道，恰能做圆周运动．C点在B点的正上方，D点为轨道的最低点．小物块离开D点后，做平抛运动，恰好垂直于倾斜挡板打在挡板跟水平面相交的E点．已知半圆轨道的半径R=0.9m，D点距水平面的高度h=0.75m，取g=10m/s2，试求：
（1）摩擦力对物块做的功；
（2）小物块经过D点时对轨道压力的大小；
（3）倾斜挡板与水平面间的夹角θ．

参考答案：（1）设小物块经过C点时的速度大小v1，因为经过C时恰好能完成圆周运动，由牛顿第二定律可得：
mg=mv21R，解得v1=3m/s
小物块由A到B过程中，设摩擦力对小物块做的功为W，由动能定理得：
W=12mv21，解得W=4.5J
故摩擦力对物块做的功为4.5J．
（2）设小物块经过D点时的速度为v2，对由C点到D点的过程，由动能定理的：
mg.2R=12mv22-12mv21
小物块经过D点时，设轨道对它的支持力大小为FN，由牛顿第二定律得：
FN-mg=mv22R
联立解得FN=60N，v2=3

本题解析：

本题难度：简单

3、选择题  A、B两物体的速度之比为2∶1，质量的大小之比为1∶3，则它们的动能之比为
A.12∶1
B.4∶3
C.12∶5
D.4∶3

参考答案：D

本题解析：

本题难度：困难

4、计算题  （18分）如图所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R="0.45" m
的1/4圆弧面,A和D分别是圆弧的端点,BC段表面粗糙,其余段表面光滑,小滑块P1和P2的质量均为m,滑板的质量M=4m.P1和P2与BC面的动摩擦因数分别为μ1=0.10和μ2=0.40,最大静摩擦力近似等于滑动摩擦力,开始时滑板紧靠槽的左端,P2静止在粗糙面的B点。P1以v0="4.0" m/s的初速度从A点沿弧面自由滑下,与P2发生弹性碰撞后,P1停在粗糙面B点上,当P2滑到C点时,滑板恰好与槽的右端碰撞并与槽牢固粘连,P2继续滑动,到达D点时速度为零,P1与P2可视为质点,取g="10" m/s2。问：

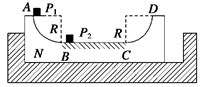
（1）P2在BC段向右滑动时,滑板的加速度为多大？
（2）BC长度为多少？N、P1和P2最终静止后,P1与P2间的距离为多少？

参考答案：（1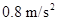）（2）1.9m? 0.695m

本题解析：　(1) P2在BC段向右滑动时，P1停在粗糙面B点上。将N、P1看作整体，根据牛顿第二定律得：
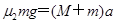?①
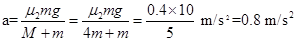?②
(2)设P1到达B点的速度为v，P1 从A点到达B点的过程中，根据动能定理有：
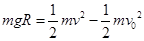?③
代入数据得?④
因P1、P2质量相等且发生弹性碰撞，所以碰后P1、P2交换速度，即碰后P2在B点的速度为：
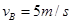?⑤
设P2在C点的速度为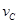，P2从C点到D点过程中根据动能定理得：
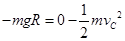?⑥
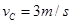代入数据得?⑦
P2从B点到C点的过程中，N、P1、P2作为一个系统所受合外力为零，系统动量守恒，设P2到达C点时N和P1的共同速度为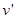.根据动量守恒定律得：
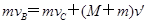?⑧
v′为滑板与槽的右端粘连前滑板和P1的共同速度．对P2从B点到C点相对地面位移为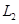由动能定理
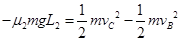?⑨
P1 和N作为一个整体，相对地面位移为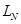，根据动能定理则有
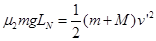?⑩
联立⑧⑨⑩得BC长度
?
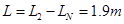滑板与槽粘连后，P1在BC上移动的距离为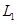，根据动能定理
?
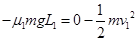P2在D点滑下后，在BC上移动的距离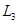，根据动能定理有
?
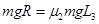联立得系统完全静止时P1与P2的间距?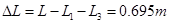
⑥⑧⑨⑩各2分，其余各1分

本题难度：一般

5、选择题   如图所示，一个小球(视为质点)从H＝12 m高处，由静止开始沿光滑弯曲轨道AB，进入半径R＝4 m的竖直圆环内侧，且与圆环的动摩擦因数处处相等，当到达圆环顶点C时，刚好对轨道压力为零；然后沿CB圆弧滑下，进入光滑弧形轨道BD，到达高度为h的D点时速度为零，则h的值可能为

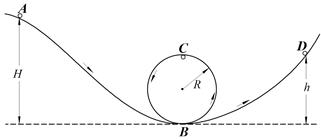
A．10 m　　　
B．9.5 m
C．8.5 m
D．8 m

参考答案：BC

本题解析：小球到达环顶C时，刚好对轨道压力为零，在C点，由重力充当向心力，则
根据牛顿第二定律得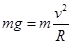：,因R=4m，小球在C点时的动能为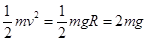
以B点为零势能面，小球重力势能Ep=2mgR=8mg．开始小球从H="12m" 高处，由静止开始通过光滑弧形轨道AB，因此在小球上升到顶点时，根据动能定理得：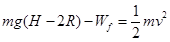
所以摩擦力做功Wf=2mg，此时机械能等于10mg，之后小球沿轨道下滑，由于机械能有损失，所以下滑速度比上升速度小，因此对轨道压力变小，所受摩擦力变小，所以下滑时，摩擦力做功大小小于2mg，机械能有损失，到达底端时小于10mg；此时小球机械能大于10mg-2mg=8mg，而小于10mg，所以进入光滑弧形轨道BD时，小球机械能的范围为，8mg＜Ep＜10mg，所以高度范围为8m＜h＜10m，故BC正确．

本题难度：一般