微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,在光滑水平面上停放着质量为m装有光滑弧形槽的小车,一个质量也为m的小球以水平速度v0沿槽口向小车滑去,到达某一高度后,小球又返回右端,则(? )

A.小球以后将向右做平抛运动
B.小球将做自由落体运动
C.此过程小球对小车做的功为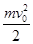
D.小球在弧形槽上升的最大高度为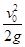
参考答案:B C
本题解析:
试题分析:小球从地段进入圆弧槽,到达最高点后返回到低端时 两者交换速度,即小球的速度减少为零,小车的速度变为v0, 小球以后将做自由落体运动,A错B对;此过程中小球对小车做的功等于小车动能的增量即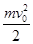 ,C选项正确;小球上升到最高点时达到共速v,根据动量守恒 mv0=2mv,解得v=v0/2,根据能量守恒定律
,C选项正确;小球上升到最高点时达到共速v,根据动量守恒 mv0=2mv,解得v=v0/2,根据能量守恒定律 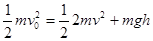 ,解得
,解得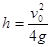 ,选项D错误。
,选项D错误。
本题难度:一般
2、选择题 不定项选择
如图所示,两块小木块A和B,中间夹上轻弹簧,用线扎在一起,放在光滑的水平台面上,烧断线,弹簧将木块A、B弹出,最后落到水平地面上,根据图中的有关数据,可以判定下列说法中正确的有(弹簧原长远小于桌面长度)( ? )
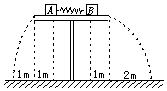
A.木块A先落到地面上
B.弹簧推木块时,两木块加速度之比aA∶aB=1∶2
C.从烧断线时到两木块滑离桌面前,两木块各自所受合冲量之比IA∶IB=l∶2
D.两木块在空中飞行时所受的冲量之比IA′∶IB′=2∶1
参考答案:BD
本题解析:
本题难度:一般
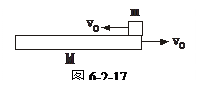
3、计算题 如图6-2-17所示,已知光滑水平面上有质量为M的长板正以速度v0向右运动,某时刻,质量为m的木块以与M等大的速度v0从长板右端进入长板上面向左运动,m<M.已知木块没有滑离长板且最后木块和长板相对静止,求从木块滑上长板到木块与长板相对静止的过程中,木块和长板相对水平面的位移大小之比为多少?
参考答案: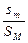 =
=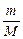
本题解析:由于M>m,Mv0>mv0,所以,最终M和m以相同的速度向右运动.即m先向左做匀减速运动,速度减到零后再向右做匀加速运动,直到和长板达到共同速度,长板一直向右做匀减速运动,直到和木块达到共同速度,之后它们一起做匀速运动.所以,木块的最小速度为零,长板的最小速度为它们一起匀速运动的速度v,由动量守恒定律得
Mv0-mv0=(M+m)v,解得v=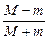 v0;
v0;
在它们相对运动的过程中,木块位移的大小为sm=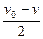 t=
t=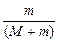 v0t
v0t
长板位移大小为sM=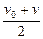 t=
t=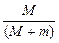 v0t
v0t
它们相对水平面的位移之比为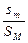 =
=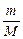 .
.
本题难度:一般
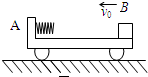
4、简答题 如图所示,质量为M的小车A左端固定一根轻弹簧,车静止在光滑水平面上,一质量为m的小物块B从右端以速度v0冲上小车并压缩弹簧,然后又被弹回,回到车右端时刚好与车保持相对静止.求:
(1)这过程弹簧的最大弹性势能EP为多少?
(2)全过程系统摩擦生热Q多少?
参考答案:(1)全过程系统动量守恒,小物块将弹簧压缩到最短和被弹回到车右端的两个时刻,系统的速度是相同的,设向左为正方向:
mv0=(M+m)v
由于两个时刻速度相同,说明小物块从车左端返回车右端过程中弹性势能的减小恰好等于系统内能的增加,即弹簧的最大弹性势能Ep恰好等于返回过程的摩擦生热,而往返两个过程中摩擦生热是相同的,所以EP是全过程摩擦生热Q的一半,Q=2EP
全过程由能量守恒和转过定律得:
Q=12mv02-12(M+m)v2
联立得:EP=Mmv024(m+M)
Q=Mmv022(m+M)
答:(1)这过程弹簧的最大弹性势能EP为Mmv024(m+M);
(2)全过程系统摩擦生热Q为Mmv022(m+M).
本题解析:
本题难度:一般
5、计算题 如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h。物块B质量是小球的5倍,置于粗糙的水平面上且位于O点正下方,物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为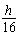 。小球与物块均视为质点,不计空气阻力,重力加速度为g,求碰后物块的速度。
。小球与物块均视为质点,不计空气阻力,重力加速度为g,求碰后物块的速度。

参考答案:解:设小球的质量为m,运动到最低点与物块碰撞前的速度大小为v1,取小球运动到最低点重力势能为零,根据机械能守恒定律,有
mgh=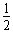 mv12 ①
mv12 ①
得v1=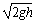
设碰撞后小球反弹的速度大小为v′1,同理有
mg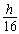 =
=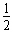 mv′12 ②
mv′12 ②
得v′1=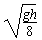
设碰后物块的速度大小为v2,取水平向右为正方向,根据动量守恒定律,有
mv1=-mv′1+5mv2 ③
得v2= ④
④
本题解析:
本题难度:困难