1、计算题  （18分）如图在xoy平面内有平行于x轴的两个足够大的荧光屏M、N，它们的位置分别满足y=l和y=0，两屏之间为真空区域。在坐标原点O有一放射源不断沿y轴正方向向真空区域内发射带电粒子，已知带电粒子有两种。为探索两种粒子的具体情况，我们可以在真空区域内控制一个匀强电场和一个匀强磁场，电场的场强为E，方向与x轴平行，磁场的磁感应强度为B，方向垂直于xoy平面。
试验结果如下：如果让电场和磁场同时存在，我们发现粒子束完全没有偏转，仅在M屏上有一个亮点，其位置在S（ 0 , l ）；如果只让磁场存在，我们发现仅在N屏上出现了两个亮点，位置分别为P（ -2l ， 0 ）、Q（ ，0 ），由此我们可以将两种粒子分别叫做P粒子和Q粒子。已知粒子间的相互作用和粒子重力可以忽略不计，试求（坐标结果只能用l表达）：

（1）如果只让磁场存在，但将磁场的磁感应强度减为B1= 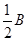，请计算荧光屏上出现的所有亮点的位置坐标；
（2）如果只让电场存在，请计算荧光屏上出现的所有亮点的位置坐标；
（3）如果只让磁场存在，当将磁场的磁感应强度变为B2= kB时，两种粒子在磁场中运动的时间相等，求k的数值。

参考答案：（1）P粒子亮点位置（，l ）? Q粒子仍打在N屏上，易得亮点位置（l，0）
（2）（，l）、（-2l，l） （3）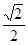

本题解析：（1）当磁场B和电场E同时存在时，两种粒子都受力平衡，都满足
Eq=Bqv
所以两种粒子速度相同都为v=? ①（2分）
当仅存在磁场时，带电粒子做匀速圆周运动，洛仑兹力充当向心力，两种粒子都满足
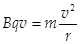得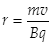? ②（2分）
当磁场强度为B时，
P粒子的轨道半径r1=l，Q粒子轨道半径为r2=? ③
由②可知当磁场为B1减半时，两粒子做圆周运动的半径都加倍，此时 r1′=2l，r2′=
此时P粒子将打在M屏上，由几何关系可求出落点横坐标

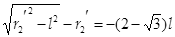
所以P粒子亮点位置（，l ）?（1分）
而Q粒子仍打在N屏上，易得亮点位置（l，0）?（1分）

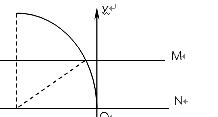
（2）由上问①②③式，可得两粒子的荷质比及其与E、B的关系，对P、Q分别有
?④
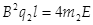? ⑤（1分）
当仅存在电场时，P粒子将向右偏，y方向分运动为匀速直线运动
vt=l? ⑥（1分）
x方向分运动为受电场力下的匀加速直线运动，有
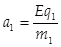? ⑦
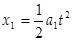? ⑧（1分）
结合④⑥⑦可得
? ⑨（1分）
由①④⑨可得
x1=
同理可以求得Q粒子在-x方向的偏转位移为
x2=2l?
故P、Q两粒子打在屏上的位置坐标分别为（，l）、（-2l，l）。?（2分）
（3）由②和③可以得出结论，不论磁场为多少，P、Q两粒子的轨道半径R1：R2=4：1不变。因为两粒子速度大小相等，所以要想两粒子运动时间相等，即运动弧长相等，两粒子运动的圆弧圆心角之比必须为θ1：θ2=1：4。
如图粒子打在M屏上时，其运动轨迹圆弧圆心角θ（锐角）与半径R满足l=Rsinθ，不可能满足R1：R2=4：1和θ1：θ2=1：4。所以两粒子都打在M屏上不可能满足要求。?（2分）
两粒子都打在N屏上，圆心角都为π也不能满足要求。?（2分）
所以结果必然为P粒子打在M屏而Q粒子打在N屏，所以θ2=π，而θ1=。
由几何关系易得此时R1=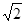l，结合②③可求得此时
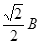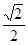B2=?，k=?（2分）

本题难度：一般

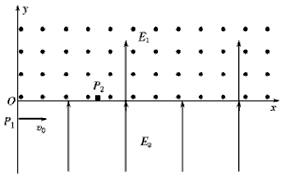
2、计算题  如图所示，坐标系中第一象限有垂直纸面向外的匀强磁场，磁感应强度B=102 T，同时有竖直向上与y轴同方向的匀强电场，场强大小E1=102 V/m，第四象限有竖直向上与y轴同方向的匀强电场，场强大小E2=2E1=2×102 V/m。若有一个带正电的微粒，质量m=10-12 kg，电量q=10-13 C，以水平与x轴同方向的初速度从坐标轴的P1点射入第四象限，OP1=0.2 m，然后从x轴上的P2点穿入第一象限，OP2=0.4 m，接着继续运动。取g=10 m/s2。求：
(1)微粒射入的初速度；
(2)微粒第三次过x轴的位置；
(3)从P1开始到第三次过x轴的总时间。

参考答案：解：(1)微粒从P1到P2做类平抛运动，由于qE2=2mg，则加速度a=g，则运动时间t1==0.2 s
微粒射入的初速度：v0=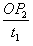=2 m/s

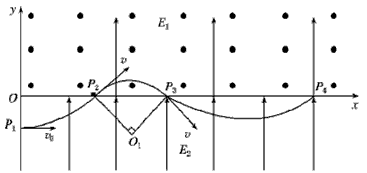
(2)微粒进入第一象限的速度：v=m/s
粒子运动方向与x轴夹角为45°
由qE1=mg，则微粒进入第一象限做匀速圆周运动，则圆周运动的半径R=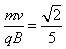m
P2P3=2Rcos45°=0.4 m
圆周运动的时间t2=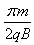=0.157 s
微粒再次进入第四象限做类斜上抛运动，由运动的分解可知：x轴方向做匀速运动，y轴方向做类上抛运动，粒子的运动时间t3=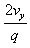=0.4 s
运动距离P3P4=vxt3=0.8 m
故OP4=OP2+P2P3+P3P4=1.6 m
微粒第三次过x轴的位置距O点1.6 m处
(3)求(2)知t=t1+t2+t3=0.757 s

本题解析：

本题难度：困难

3、计算题  有人设想用下图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电，电量与其表面积成正比。电离后，粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域1，再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II，其中磁场的磁感应强度大小为B，方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子，其质量为m0、电量为q0，刚好能沿O1O3直线射入收集室。不计纳米粒子重力。（）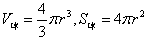
（1）试求图中区域II的电场强度；
（2）试求半径为r的粒子通过O2时的速率；
（3）讨论半径r≠r0的粒子刚进入区域II时向哪个极板偏转。

参考答案：解：（1）设半径为r0的粒子加速后的速度为v0，则

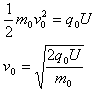
设区域II内电场强度为E，则

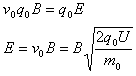
电场强度方向竖直向上
（2）设半径为r的粒子的质量为m、带电量为q、被加速后的速度为v，则
?
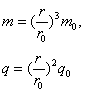由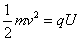得
（3）半径为r的粒子，在刚进入区域II时受到合力为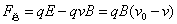
由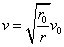可知，当
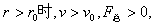粒子会向上极板偏转；
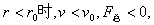粒子会向下极板偏转；

本题解析：

本题难度：困难

4、计算题  如图所示，两根足够长、相距为L的金属直角导轨，它们各有一边在同一水平面内，另一边垂直于水平面。一绝缘细线跨过导轨直角顶点处定滑轮连接两金属细杆ab、cd，杆通过两端金属小圆环垂直套在导轨上，细杆质量均为m、电阻均为R，整个装置处于磁感强度大小为B，方向竖直向上的匀强磁场中。保持细线拉直后同时无初速释放两细杆，cd杆下降高度h时达到最大速度。 ab杆一直在水平导轨上运动，接触处摩擦及导轨电阻均不计，取重力加速度为g。求：

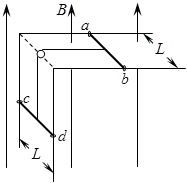
(1)刚释放时，ab杆的加速度大小；
(2)下滑过程中，cd杆的最大速率；
(3)从开始释放到刚好达到最大速度的过程中整个回路所产生的热量。

参考答案：（1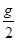）?（2）?（3）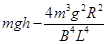

本题解析：(1)刚开始运动时，对系统根据牛顿第二定律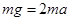：得：
(2) ab在运动中切割磁感线产生电动势：?
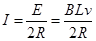
受安培力：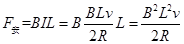
对系统根据牛顿第二定律：
速率最大时加速度为零：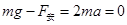
解得：
(3)对系统利用动能定理：
产生的热量：

本题难度：一般

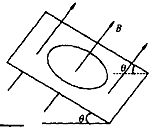
5、填空题  如图所示，倾角为θ的光滑绝缘斜面，处在方向垂直斜面向上的匀强磁场和方向未知的匀强电场中，有一质量为m、带电量为-q的小球，恰可在斜面上做匀速圆周运动、其角速度为ω，那么，匀强磁场的磁感应强度的大小为___________，未知电场的最小场强的大小为____________，方向沿_____________。

参考答案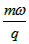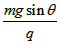：；；沿斜面向下

本题解析：

本题难度：一般