微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 如图所示,PQ是一长为L=0.64m的绝缘平板,固定在水平地面上,挡板K固定在平板的右端。整个空间有一个平行于PQ的匀强电场E,在板的右半部分有一垂直于纸面向里的匀强磁场,磁场的宽度d=0.32m。一个质量m=0.50×10-3 kg、带电荷量为q=5.0×10-2 C的小物体(可视为质点),从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动。当物体碰到挡板K后被弹回,若在碰撞瞬间撤去电场(不计撤去电场对原磁场的影响),物体返回时在磁场中仍作匀速运动,离开磁场后做减速运动,停在C点,PC=L/4。若物体与平板间的动摩擦因数μ=0.20,g取10m/s2。
(1)判断电场的方向及物体带正电还是带负电;
(2)求磁感应强度B的大小;
(3)求物体与挡板碰撞过程中损失的机械能。
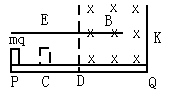
参考答案:解:(1)物体由静止开始向右做匀加速运动,证明电场力向右且大于摩擦力。进入磁场后做匀速直线运动,说明它受的摩擦力增大,证明它受的洛伦兹力方向向下。由左手定则判断,物体带负电。物体带负电而所受电场力向右,证明电场方向向左
(2)设物体被挡板弹回后做匀速直线运动的速度为v2,从离开磁场到停在C点的过程中,根据动能定理有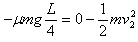
解得
物体在磁场中向左做匀速直线运动,
解得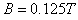
(3)设从D点进入磁场时的速度为v1,根据动能定理有: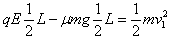
物体从D到R做匀速直线运动,受力平衡: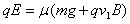
解得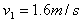
小物体撞击挡板损失的机械能为: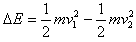
解得
本题解析:
本题难度:一般
2、计算题 (16分)如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,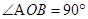 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = a,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = a,不计粒子的重力。求:

(1)匀强电场的电场强度E的大小;
(2)为使粒子能从M点经Ⅱ区域通过OB上的N点,M、N点关于y轴对称,可在区域Ⅱ内加一垂直xOy平面的匀强磁场,求该磁场的磁感应强度的最小值和粒子经过区域Ⅲ到达x轴上Q点的横坐标;
(3)当匀强磁场的磁感应强度取(2)问中的最小值时,且该磁场仅分布在一个圆形区域内。由于某种原因的影响,粒子经过M点时的速度并不严格与OA垂直,成散射状,散射角为 ,但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
,但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
参考答案:(1)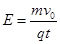 (2)(
(2)( ,0)(3)2
,0)(3)2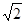 v0tsinθ
v0tsinθ
本题解析:(1)粒子在Ⅰ区域内做类平抛运动,
 ?(1分)
?(1分)
vx= v0?(1分)
解得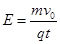 ?(1分)
?(1分)
(2) 粒子在Ⅰ区域内在y方向上的位移y1= v0t?(1分)
OM=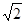 y1=
y1=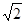 v0t?(1分)
v0t?(1分)
粒子在Ⅱ区域内做匀速圆周运动,其轨道半径R≤OM1=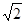 v0t?(1分)
v0t?(1分)
又因为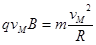 ?(1分)
?(1分)
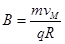 ≥
≥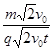 =
= ,即Bmin=
,即Bmin= ?(1分)
?(1分)
粒子进入Ⅲ区域后,其运动轨迹NQ与PQ对称,则OQ=OP=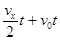 =
=
所以Q点的坐标为( ,0)?(1分)
,0)?(1分)
速度方向沿负y方向?(1分)
(3)该圆形磁场区域的半径r等于其轨迹圆半径R,即r=R=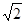 v0t?(2分)
v0t?(2分)
所有粒子出磁场时速度方向平行,其落点在直线OB上的GH两点之间,如图(2分)

GH=2rsinθ=2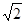 v0tsinθ?(2分)
v0tsinθ?(2分)
本题难度:一般
3、选择题 如图所示,相距为d的两平行金属板水平放置,开始开关S1和S2均闭合使平行板电容器带电。板间存在垂直纸面向里的匀强磁场。一个带电粒子恰能以水平速度v向右匀速通过两板间。在以下方法中,有可能使带电粒子仍能匀速通过两板的是(不考虑带电粒子所受重力)

[? ]
A.保持S1和S2均闭合,减小两板间距离,同时减小粒子射入的速率
B.保持S1和S2均闭合,将R1、R3均调大一些,同时减小板间的磁感应强度
C.把开关S2断开,增大两板间的距离,同时减小板间的磁感应强度
D.把开关S1断开,增大板间的磁感应强度,同时减小粒子入射的速率
参考答案:B
本题解析:
本题难度:一般
4、实验题 如图所示,在互相垂直的水平方向的匀强电场(E已知)和匀强磁场(B已知)中,有一固定的竖直绝缘杆,杆上套有一个质量为m、电荷量为+q的小球,它们之间的动摩擦因数为μ.现由静止释放小球,则小球运动的加速度________________,速度________________.(填变化情况),其最大速度vm=________________.(已知mg>μEq).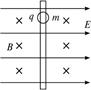
参考答案:一直减小(直至为0)?先增大后不变?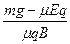
本题解析:开始小球受力见图(a),N=Eq,由题意知mg>μEq,所以小球加速向下运动,以后小球受洛伦兹力(如图b),相应N、f均增加,小球加速度减小,速度仍在增加,只是增加得慢了,洛伦兹力、弹力、摩擦力将随之增加,合力继续减小,直到加速度a=0时,小球速度达到最大值后匀速运动,有:mg=μ(Eq+qvmB),vm= .
.
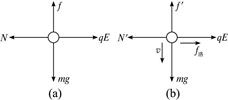
本题难度:简单
5、计算题 如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B。在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场。不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收。
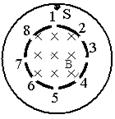
(1)一质量为m1,带电量为+q1的粒子从紧靠外筒且正对1号缝的S点由静止出发,进入磁场后到达的第一个狭缝是3号缝,求两电极间加的电压U是多少?
(2)另一个粒子质量为m2,带电量为+q2,也从S点由静止出发,该粒子经过一段时间后恰好又回到S点,求该粒子在磁场中运动多少时间第一次回到S点。
参考答案:(1) (2)第一种情况
(2)第一种情况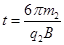 ;第二种情况
;第二种情况 ;第三种情况
;第三种情况 ;
;
本题解析:(1)m1粒子从S点出发在电场力作用下加速沿径向由1号缝以速度V1进入磁场,
依动能定理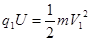 ?①
?①
在磁场中做匀速圆周运动,由洛伦兹力公式和牛顿定律得
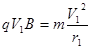 ?②?
?②?
粒子从1号缝直接到3号缝,轨迹为1/4圆周,轨迹半径等于内筒半径
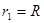 ?③?
?③?
由以上得 ?④?
?④?
(2)m2粒子进入磁场后,做匀速圆周运动周期为T?
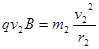 ?⑤?
?⑤?
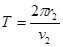 ?⑥?
?⑥?
得?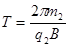 ?⑦?
?⑦?
m2粒子能回到S点的条件是能沿径向进入某条缝,在电场中先减速再反向加速重回磁场,然后以同样的方式经过某些缝最后经1号缝回到S点。共有三种可能情况
第一种:粒子依次经过2、3、4、5、6、7、8号缝回到1号缝

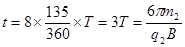 ?⑧?
?⑧?
第二种:粒子依次经3、5、7号缝回到1号缝

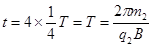 ⑨?
⑨?
第三种:粒子依次经过4、7、2、5、8、3、6号缝回到1号缝
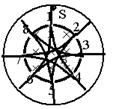
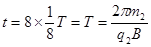 ?⑩
?⑩
本题难度:一般
Learn young, learn fair. 学习趁年少,而且要学好.