|
高考物理试题《粒子在有界磁场中运动》试题强化练习(2017年最新版)(六)
2017-07-10 21:29:41
来源:91考试网
作者:www.91exam.org 【 大 中 小】
|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,圆形区域内有垂直纸面向内的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力的作用,则下列说法错误的是( )
A.三个粒子都带正电荷
B.c粒子速率最小
C.c粒子在磁场中运动时间最短
D.它们做圆周运动的周期Ta=Tb=Tc
|
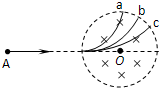
参考答案:A、三个带电粒子均向上偏转,射入磁场时所受的洛伦兹力均向上,根据左手定则判断得知:三个粒子都带正电荷.故A正确.
B、粒子在磁场中做匀速圆周运动时,由洛伦兹力提供向心力,根据qvB=mv2r,可得:r=mvqB,则可知三个带电粒子的质量、电荷量相同,在同一个磁场中,当速度越大时、轨道半径越大,则由图知,a粒子的轨迹半径最小,c粒子的轨迹半径最大,则a粒子速率最小,c粒子速率最大,故B错误,
C、D三个带电粒子的质量和电荷量都相同,由粒子运动的周期 T=2πmqB及 t=θ2πT,θ是粒子轨迹对应的圆心角,也等于速度的偏转角,可知,三粒子运动的周期相同,即Ta=Tb=Tc.
由图知,a在磁场中运动的偏转角最大,运动的时间最长,c在磁场中运动的偏转角最小,c粒子在磁场中运动时间最短,故CD正确.
本题选错误的,故选:B.
本题解析:
本题难度:简单
2、选择题 如右图所示,带有正电荷的A粒子和B粒子同时以同样大小的速度从宽度为d的有界匀强磁场的边界上的O点分别以30°和60°(与边界的交角)射入磁场,又恰好不从另一边界飞出,则下列说法中正确的是?(?)

A.A、B两粒子在磁场中做圆周运动的半径之比是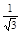
B.A、B两粒子在磁场中做圆周运动的半径之比是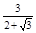
C.A、B两粒子的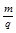 之比是 之比是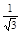
D.A、B两粒子的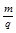 之比是 之比是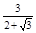
参考答案:BD
本题解析:RAcos30°+RA=d,RBcos60°+RB=d,,解得 ,A错B对;因 ,A错B对;因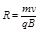 ,故 ,故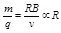 ,故 ,故 ,C错D对 ,C错D对
本题难度:一般
3、计算题 电子质量为m,电荷量为e,从坐标原点O处沿xOy平面射入第一象限,射入时速度方向不同,速度大小均为v0,如图所示。现在某一区域加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度为B,若这些电子穿过磁场后都能垂直射到荧光屏MN上,荧光屏与y轴平行,求:
(1)荧光屏上光斑的长度;
(2)所加磁场范围的最小面积。
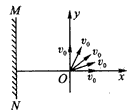
参考答案:解:(1)如图所示,求光斑长度,关键是找到两个边界点,初速度方向沿x轴正方向的电子,沿弧OB运动到P;初速度方向沿y轴正方向的电子,沿弧OC运动到Q
电子在磁场中的半径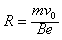
由图可知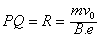
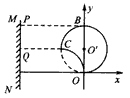
(2)沿任一方向射入第一象限的电子经电场偏转后都能垂直打到荧光屏MN上,所加最小面积的磁场的边界是以O"(0,R)为圆心,R为半径的圆的一部分,如图中实线所示,所以磁场范围的最小面积为
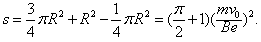
本题解析:
本题难度:困难
4、选择题 如图所示,在I、II两个区域内存在磁感应强度均为B的匀强磁场,磁场方向分别垂直于纸面向 外和向里,AD、AC边界的夹角∠DAC=300,边界AC与 边界MN平行,II区域宽度为d。质量为m、电荷量为十q的粒子可在边界AD上的不同点射人,入射速度垂直AD且垂直磁场,若入射速度大小为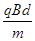 ?,不计粒子重力,则 ?,不计粒子重力,则
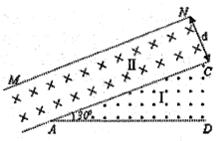
A.粒子在磁场中的运动半径为
B.粒子距A点0.5d处射入,不会进入II区
C.粒子距A点1.5d处射入,在I区内运动的时间为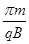
D.能够进入II区域的粒子,在II区域内运动的最短时间为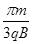
参考答案:CD
本题解析:粒子在磁场中做圆周运动的向心力由洛伦兹力提供,则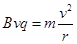 ,解得 ,解得 ,选项A 错误;粒子距A点0.5d处射入时,圆心在AD上距离A点为1.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子不会进入II区,选项B错误;粒子距A点1.5d处射入,圆心在AD上距离A点为2.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子在I区将做半个圆周运动而射出,所以运动的时间为 ,选项A 错误;粒子距A点0.5d处射入时,圆心在AD上距离A点为1.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子不会进入II区,选项B错误;粒子距A点1.5d处射入,圆心在AD上距离A点为2.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子在I区将做半个圆周运动而射出,所以运动的时间为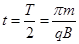 ;因为能够进入II区域的粒子的运动半径等于在I区域内的运动半径,若在II区域内运动的最短,则需弦长最短,而最短的弦长为d,此弦长所对圆心角为 ;因为能够进入II区域的粒子的运动半径等于在I区域内的运动半径,若在II区域内运动的最短,则需弦长最短,而最短的弦长为d,此弦长所对圆心角为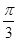 ,所以运动的时间为 ,所以运动的时间为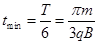 ,选项D 正确。 ,选项D 正确。
本题难度:一般
5、计算题 如图13所示在平面直角坐标系xOy中,,第Ⅰ、II象限存在沿y轴负方向的匀强电场,场强大小为E,第III、Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上距原点O为d的P点以速度v0垂直于y轴射入第Ⅰ象限的电场,经x轴射入磁场,已知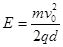 , ,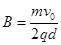 .不计粒子重力,求: .不计粒子重力,求:
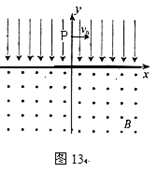
(1)粒子在磁场中运动的半径,画出带电粒子运动的轨迹。
(2)从粒子射入电场开始,求粒子经过x轴时间的可能值。
参考答案:(1)见解析
(2)带电粒子经过x轴正半轴时间的可能值为
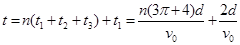 (n=0、1、2、3…). (n=0、1、2、3…).
带电粒子经过x轴负半轴时间的可能值为
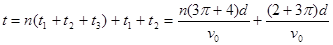 (n=0、1、2、3…). (n=0、1、2、3…).
本题解析:(1)带电粒子射入电场中作类平抛运动,由牛顿第二定律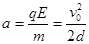 ① ①
由类平抛运动的特点,竖直方向上作初速为零的匀加速运动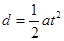 ②, ②,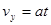 ③ ③
水平方向上作匀速运动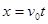 ④ ④
设合速度与水平方向的夹角为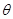 ,由合速度与分速度的关系得 ,由合速度与分速度的关系得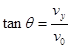 ⑤ ⑤
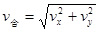 ⑥ ⑥
以上六式联立可得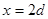 , ,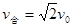 , ,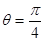 . .
带电粒子在磁场中作匀速圆周运动,洛伦兹力提供向心力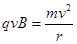 ⑦,代入可得 ⑦,代入可得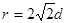 ⑧ ⑧
由几何关系可确定出带电粒子在磁场中做圆周运动的圆心在y轴下方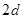 处,根据圆的对称性,粒子出磁场时的速度和距离与入时对称,带电粒子进入第II象限作斜抛运动,运动情况跟在第一像限对称,故可画出带电粒子运动的轨迹。 处,根据圆的对称性,粒子出磁场时的速度和距离与入时对称,带电粒子进入第II象限作斜抛运动,运动情况跟在第一像限对称,故可画出带电粒子运动的轨迹。

①②③④⑤⑥⑦⑧每式1分,轨迹3分,共11分.
(2)由上问知粒子在第Ⅰ象限的电场中运动的时间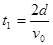 ①,在磁场中运动的周期由 ①,在磁场中运动的周期由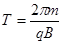 ,带电粒子在磁场中运动的时间为 ,带电粒子在磁场中运动的时间为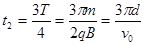 ②,带电粒子在第第II象限的电场中运动的时间 ②,带电粒子在第第II象限的电场中运动的时间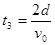 ③,故带电粒子经过x轴正半轴时间的可能值为 ③,故带电粒子经过x轴正半轴时间的可能值为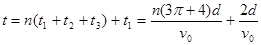 (n=0、1、2、3…)④. (n=0、1、2、3…)④.
带电粒子经过x轴负半轴时间的可能值为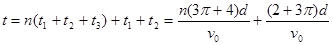 (n=0、1、2、3…)⑤. (n=0、1、2、3…)⑤.
①②③每式1分, ④⑤每式2分,共7分.
本题难度:一般
| 