1、简答题  如图所示，滑块A、B的质量分别为
m1与m2，m1＜m2，由轻质弹簧相连接置于水平的气垫导轨上，用一轻绳把两滑块拉至最近，使弹簧处于最大压缩状态后绑紧。
两滑块一起以恒定的

参考答案：
小题1:Ep=(m1-m2)(m1+m2)v02/2m2.
小题2:不可能

本题解析：
小题1:当弹簧处压缩状态时，系统的机械能等于两滑块的动能和弹簧的弹性势能之和，当弹簧伸长到自然长度时，弹性势能为0，因这时滑块A的速度为0，故系统的机械能等于滑块B的动能.设这时滑块B的速度为v，则有E=m2v2/2.
因系统所受外力为0，由动量守恒定律
(m1+m2)v0=m2v.
解得E=(m1+m2)2v02/(2m2).
由于只有弹簧的弹力做功，系统的机械能守恒
(m1+m2)v02/2+Ep=E.
解得Ep=(m1-m2)(m1+m2)v02/2m2.
小题2:假设在以后的运动中滑块B可以出现速度为0的时刻，并设此时A的速度为v1，弹簧的弹性势能为E′p，由机械能守恒定律得
m1v12/2+E′p=(m1+m2)2v02/2m2.
根据动量守恒得(m1+m2)v0=m1v1，
求出v1代入上式得:
(m1+m2)2v02/2m1+E′p=(m1+m2)2v02/2m2.
因为E′p≥0，故得:
(m1+m2)2v02/2m1≤(m1+m2)2v02/2m2
即m1≥m2，这与已知条件中m1＜m2不符.
可见在以后的运动中不可能出现滑块B的速度为0的情况.

本题难度：一般

2、选择题  一辆小车在光滑地面上匀速滑行（空气阻力不计），以下几种情形中，小车的速度仍保持不变的有
A．车外的物体自空中竖直落入车内
B．车厢内的砂粒持续地从车厢底部的缝隙处漏到车外
C．从车上同时向前、向后以对地相同的速率抛出等质量的两物
D．从地上同时向前、向后以相同的速率向车中抛入等质量的两物

参考答案：B

本题解析：这个题目考查学生灵活运用“动量守恒定律”，灵活选取研究对象分析具体问题的能力。
考查知识点：动量守恒定律
思路分析：分析选项中研究对象的变化情况，利用动量守恒定律即可
具体解答过程：选取车、车外的物体为系统，设车、车外的物体的质量分别为M、m，物体落到车前、后的速度分别为V。、V，则M V。=（M+m）V，可知A错误。
车厢内的砂粒持续地从车厢底部的缝隙处漏到车外，选取除去沙粒的车为研究对象，可知它的动量不变，B正确。
设抛出的物体的质量为m1，则M V。=（M-2m1）V，可知C错误。
设抛入等质量的两物体质量为m2，速率为v2，则从地上同时向前、向后以相同的速率向车中前后，M V。=（M+2m2）V，可知D错误。
试题点评：学生正确选取研究对象，正确运用动量守恒定律很关键。

本题难度：一般

3、简答题  （1）如图6-15，在光滑水平长直轨道上，放着一个静止的弹簧振子，它由一轻弹簧两端各连接一个小球构成，两小球质量相等.现突然给左端小球一个向右的速度u0，求弹簧第一次恢复到自然长度时，每个小球的速度.
（2）如图6-16，将N个这样的振子放在该轨道上，最左边的振子1被压缩至弹簧为某一长度后锁定，静止在适当位置上，这时它的弹性势能为E0.其余各振子间都有一定的距离，现解除对振子1的锁定，任其自由运动，当它第一次恢复到自然长度时，刚好与振子2碰撞，此后，继续发生一系列碰撞，每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后，每个振子弹性势能的最大值.已知本题中两球发生碰撞时，速度交换，即一球碰后的速度等于另一球碰前的速度.

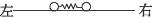
图6-15

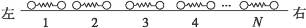
图6-16

参考答案：(1)u1=0,u2=u0? (2)EN=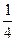E0

本题解析：（1）设每个小球质量为m，以u1、u2分别表示弹簧恢复到自然长度时左右两端小球的速度,由动量守恒和能量守恒定律有
mu1+mu2=mu0（以向右为速度正方向）
mu12+mu22=mu02
解得u1=u0,u2=0或u1=0,u2=u0
由于振子从初始状态到弹簧恢复到自然长度的过程中，弹簧一直是压缩状态，弹力使左端小球持续减速，使右端小球持续加速，因此应该取解析u1=0,u2=u0.
（2）以v1、v1′分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度，规定向右为速度的正方向，由动量守恒和能量守恒定律
mv1+mv1′=0
mv12+mv1′2=E0
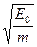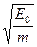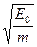解得v1=,v1′=-或v1=-,v1′=.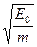
在这一过程中，弹簧一直是压缩状态，弹性力使左端小球向左加速，右端小球向右加速，故应取解析
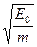v1=-,v1′=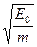
振子1与振子2碰撞后，由于交换速度，振子1右端小球速度变为0，左端小球速度仍为v1.此后两小球都向左运动，当它们向左的速度相同时，弹簧被拉伸至最长，弹性势能最大，设此速度为v10，根据动量守恒定律：
2mv10=mv1
用E1表示最大弹性势能，由能量守恒有
mv102+mv102+E1=mv12
解得E1=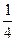E0
振子2被碰撞后瞬间，左端小球速度为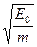，右端小球速度为0.以后弹簧被压缩，当弹簧再恢复到自然长度时，根据（1）题结果，左端小球速度v2=0，右端小球速度v2′=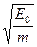，与振子3碰撞，由于交换速度，振子2右端小球速度变为0，振子2静止，弹簧为自然长度，弹性势能为E2=0.
同样分析可得
E2=E3=…=EN-1=0
振子N被碰撞后瞬间，左端小球速度vN-1′=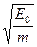，右端小球速度为0，弹簧处于自然长度.此后两小球都向右运动，弹簧被压缩，当它们向右的速度相同时，弹簧被压缩至最短，弹性势能最大.设此速度为vN0，根据动量守恒定律，
2mvN0=mvN-1′
用EN表示最大弹性势能，根据能量守恒，有
mvN02+mvN02+EN=mvN-12
解得EN=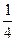E0.

本题难度：简单

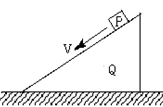
4、选择题  将物体P从置于光滑水平面上的斜面体Q的顶端以一定的初速度沿斜面往下滑，如图所示。在下滑过程中，P的速度越来越小，最后相对斜面静止，那么由P和Q组成的系统 （?）

A．动量守恒
B．水平方向动量守恒?
C．最后P和Q以一定的速度共同向左运动?
D．最后P和Q以一定的速度共同向右运动

参考答案：BC

本题解析：P和Q组成的系统竖直方向受重力做功，合外力不为零，动量不守恒，Ａ错；水平方向不受外力，水平方向动量守恒，Ｂ对；初始状态系统水平方向动量向左，末状态动量也向左，Ｃ对；Ｄ错；

本题难度：一般

5、选择题  在光滑水平面上放置一木块，一颗子弹以一定的水平初速度打入木块并穿出．如果将木块固定在水平面上，子弹穿出时的速度为v1；若木块不固定，子弹穿出时的速度为v2，设子弹穿过木块时受到的阻力相等．在这两种情况下系统的机械能损失分别为ΔE1和ΔE2，则以下正确的是
A.v1＞v2，ΔE1＝ΔE2
B.v1＞v2，ΔE1＜ΔE2
C.v1＝v2，ΔE1＝ΔE2
D.v1＜v2，ΔE1＜ΔE2

参考答案：A

本题解析：

本题难度：简单