1、填空题  场强为E、方向竖直向上的匀强电场中有两小球A、B，它们的质量分别为m１、m２，电量分别为q１、 q２．A、B两球由静止释放，重力加速度为g，则小球A和Ｂ组成的系统动量守恒应满足的关系式为　　　　　　　　　　　　．

参考答案：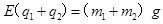

本题解析：由题意，小球A和B组成的系统动量守恒，必定满足动量守恒的条件：系统的所受合外力为零．
两球受到重力与电场力，则知电场力与重力平衡，则得：。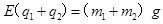
考点：考查了动量守恒定律的应用

本题难度：一般

2、选择题  质量为m的人站在质量为M、长为L的静止小船的右端，小船的左端靠在岸边（如图所示）。当他向左走到船的左端时，船左端离岸的距离是

[? ]
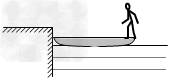
A．L?
B．?
C．?
D．?

参考答案：D

本题解析：

本题难度：一般

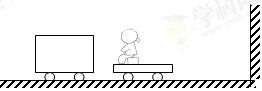
3、计算题 &nbs来源:91考试网 91eXAm.orgp;(9分)如图所示，质量为m1＝60 kg的小车在光滑水平面上以速度v1＝0.5 m/s向右运动，质量为m2＝40 kg的小车(包括小孩)在光滑水平面上以速度v2＝3 m/s向左运动，为了避免两滑块再次相碰，在两小车靠近的瞬间，m2上的小孩用力将m1推开．求小孩对m1做功的范围．(滑块m2与右边竖直墙壁碰撞时无机械能损失，小孩与小车不发生相对滑动，光滑水平面无限长)

参考答案：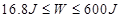

本题解析：设向左为正方向，推后二者共速向左

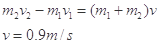
对m1分析

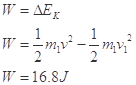
设向左为正方向，推后二者反向，速度等大


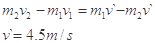
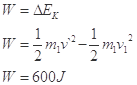
所以，做功范围为：

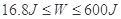
考点：原子核、动能定理、动量守恒定律

本题难度：一般

4、简答题  如图所示，甲、乙两光滑圆轨道放置在同一竖直平面内，甲轨道半径是R且为乙轨道半径的2倍，两轨道之间由一光滑水平轨道CD相连，在水平轨道CD上有一轻弹簧被a、b两个小球夹住，但不拴接．如果a、b两个小球的质量均为m，同时释放两小球，且要求a、b都能通过各自的最高点，则弹簧在释放前至少具有多大的弹性势能？

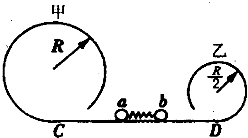
参考答案：当a球恰能通过最高点时，b球一定通过最高点，此时弹簧在释放前具有的弹性势能最小，设a球到达圆轨道最高点的速度为va，对于a球有：
mag=mav2aR…①
设a球被弹簧弹开瞬间的速度为v"a，对于a球由机械能守恒定律可得：12mav′2a=12mav2a+mag2R… ②
设b球被弹簧弹开瞬间的速度为v"b，由于a、b两球被弹开时系统动量守恒：mav"a=mbv"b …③
①②③可得：v′a=v′b=

本题解析：

本题难度：一般

5、计算题  如图所示，光滑水平面上有一小车，小车上固定一杆，总质量为M；杆顶系一长为L的轻绳，轻绳另一端系一质量为m的小球．绳被水平拉直处于静止状态(小球处于最左端)．将小球由静止释放，小球从最左端摆下并继续摆至最右端的过程中，小车运动的距离是多少？

参考答案：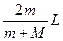

本题解析：该题立意新颖，但仔细分析与“人船模型”有相似之处，都是研究两个物体相互作用的过程，都具有水平方向合外力为零的特征，从而水平的动量守恒，初始状态球和车都处于静止状态，因此可借助“人船模型”来处理．
设某时刻小球速度的水平分量为v(方向向右)，小车的速度为V(方向向左)，取水平向左为正方向，根据动量守恒定律有：
MV－mv ="0?" 即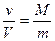
因为小球在摆动过程中，系统动量在每个时刻都等于零，所以每一时刻小球速度的水平分量与小车的速度都跟它们的质量成反比；从而可知小球从最左端摆至最右端的过程中，小球的水平位移s1与小车的位移s2与它们的质量成反比．即

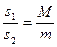
由图４知　　s1+s2=2L
由以上两式解得s2=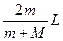
上面这题关键是找好球与船的相对位移。

本题难度：简单