微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,AB= 2BC. 小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P 由静止开始从A点释放,恰好能滑动到C 点而停下,那么θ、μ1、μ2间应满足的关系是?
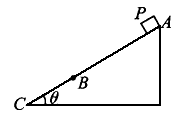
[? ]
A.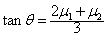
B. 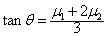
C.tanθ=2μ1-μ2
D.tanθ=2μ2-μ1
参考答案:A
本题解析:
本题难度:一般
2、简答题 如图甲所示是一打桩机的简易模型.质量m=1kg的物体在拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击钉子,将钉子打入一定深度.物体上升过程中,机械能E与上升高度h的关系图象如图乙所示.不计所有摩擦,g取10m/s2.求:
(1)物体上升1m后再经多长时间才撞击钉子(结果可保留根号);
(2)物体上升到0.25m高度处拉力F的瞬时功率.
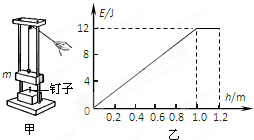
参考答案:(1)由图象可知,物体上升到h1=1m时物体的机械能:
mgh1+12mv12=12J,解得v1=2m/s;
撤去拉力后,物体做匀减速直线运动,
-h1=v1t-12gt2,解得t=
本题解析:
本题难度:一般
3、计算题 如图所示为某小区儿童娱乐的滑滑梯示意图,其中AB为斜面滑槽,与水平方向夹角为37o,BC为水平滑槽,与半径为0.2m的1/4圆弧CD相切,ED为地面.已知儿童在滑槽上滑动时的动摩擦系数都是0.5,A点离地面的竖直高度AE为2m,试求:
(1)儿童由A处静止起滑到B处时的速度大小
(2)为了使儿童在娱乐时不会从C处脱离圆弧水平飞出,水平滑槽BC长至少为多少? (B处的能量损失不计)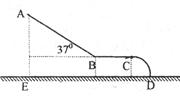
参考答案:(1)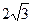 ?m/s?(3分)
?m/s?(3分)
(2)1m? (5分)
本题解析:略
本题难度:简单
4、计算题 (14分)如图所示,倾角θ = 60°的粗糙平直导轨与半径为R的光滑圆环轨道相切,切点为B,轻弹簧一端固定,自由端在B点,整个轨道处在竖直平面内。现将一质量为m的小滑块(视为质点)紧靠且压缩弹簧,并从导轨上离水平地面高h = 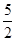 R的A处无初速下滑进入圆环轨道,恰能到达圆环最高点D,不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5,重力加速度大小为g。求:
R的A处无初速下滑进入圆环轨道,恰能到达圆环最高点D,不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5,重力加速度大小为g。求:
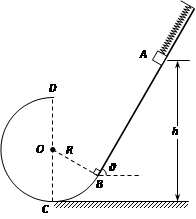
(1)滑块运动到圆环最高点D时速度υD的大小;
(2)滑块运动到圆环最低点时受到圆环轨道支持力N的大小;
(3)滑块在A处时弹簧的弹性势能Ep。
参考答案:(1)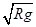 (2)N = 6mg?(2)
(2)N = 6mg?(2)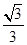 mgR
mgR
本题解析:(1)滑块恰能到达圆环最高点D,说明滑块在D点时重力恰好提供向心力,即
mg = m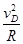 ? 2分
? 2分
得? υD = 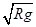 ?1分
?1分
(2)小滑块从C→D,由机械能守恒定律得
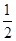 mυC2 =
mυC2 = 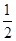 mυD2 + mg·2R? 2分
mυD2 + mg·2R? 2分
υC = 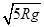 ?1分
?1分
在C点,根据牛顿第二定律,有
N– mg = m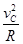 ? 2分
? 2分
得? N = 6mg? 1分
(2)AB之间长度
L = [h–(R– Rcosθ)]/sinθ= 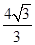 R? 1分
R? 1分
平直导轨对滑块的滑动摩擦力
f = μmgcosθ = 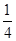 mg? 1分?
mg? 1分?
从A→C,根据能量守恒定律有
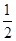 mυC2 + fL = Ep + mgh? 2分
mυC2 + fL = Ep + mgh? 2分
得? Ep = 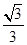 mgR? 1分
mgR? 1分
本题考查圆周运动规律的应用,在最高点通过的临界条件是只有重力提供向心力,从C到D可通过机械能守恒定律求得C点速度,在C点由支持力和重力的合力提供向心力,列式求解可得,在A到B间,通过动能定理可求得势能大小
本题难度:一般
5、简答题 如图所示,在竖直平面的xOy坐标系内,Oy表示竖直向上方向.该平面内存在沿x轴正向的匀强电场.一个带电小球从坐标原点沿Oy方向竖直向上抛出,初动能为4J,不计空气阻力.它达到的最高点位置如图中M点所示,求:(g取得m/s2)
(1)小球在M点时的动能为多少焦耳
(2)小球落回x轴时的位置N点的横坐标为多少米?
(3)小球到达N点时的动能为多少焦耳?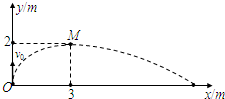
参考答案:(1)在竖直方向小球只受重力,从O→M速度由v0减小到0;在水平方向小球只受电场力,速度由0增大到v1,
由图知这两个分运动平均速度大小之比为2:3,因此v0:v1=2:3,所以小球在M点时的动能E1=94E0=9J.
(2)由竖直分运动知,O→M和M→N经历的时间相同,根据初速度为0的匀加速直线运动相邻的相等时间内的位移之比为:1:3:5:…因此水平位移大小之比为1:3,
故N点的横坐标为12.
(3)小球到达N点时的竖直分速度为v0,根据初速度为0的匀加速直线运动相邻的相等时间内的速度之比为:1:2:3:…可知水平分速度为2v1,
由此可得此时动能E2=E0+4E1=40J.
答:(1)小球在M点时的动能为9J;?(2)小球落回x轴时的位置N点的横坐标为12m;(3)小球到达N点时的动能为40J.
本题解析:
本题难度:一般