1、简答题  如图所示，光滑水平面轨道上有三个木块，A、B、C，质量分别为mB=mc=2m,mA=m，A、B用细绳连接，中间有一压缩的弹簧 (弹簧与滑块不栓接)。开始时A、B以共同速度v0运动，C静止。某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同。求B与C碰撞前B的速度。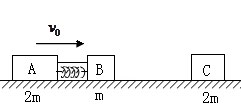

参考答案：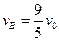

本题解析：设共同速度为v，球A和B分开后，B的速度为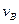,由动量守恒定律有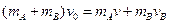,,联立这两式得B和C碰撞前B的速度为。

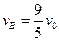本题难度：简单

2、计算题  装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击．通过对以下简化模型的计算可以粗略说明其原因．
质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板，刚好能将钢板射穿．现把钢板分成厚度均为d、质量均为m的相同两块，间隔一段距离平行放置，如图所示．若子弹以相同的速度垂直射向第一块钢板，穿出后再射向第二块钢板，求子弹射入第二块钢板的深度．设子弹在钢板中受到的阻力为恒力，且两块钢板不会发生碰撞。不计重力影响。

参考答案：

本题解析：设子弹初速度为v0，射入厚度为2d的钢板后，
由动量守恒得：mv0 =(2m＋m)V（2分）
此过程中动能损失为：ΔE损＝f·2d=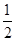mv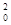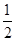－×3mV2?（2分）
解得ΔE＝mv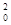
分成两块钢板后，设子弹穿过第一块钢板时两者的速度分别为v1和V1：mv1＋mV1＝mv0（2分）
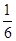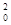因为子弹在射穿第一块钢板的动能损失为ΔE损1＝f·d=mv（1分），
由能量守恒得：
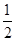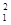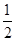mv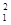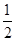＋mV＝mv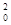－ΔE损1（2分）
且考虑到v1必须大于V1，
解得：v1＝v0
设子弹射入第二块钢板并留在其中后两者的共同速度为V2，
由动量守恒得：2mV2＝mv1（1分）
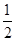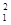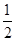损失的动能为：ΔE′＝mv－×2mV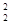?（2分）?
联立解得：ΔE′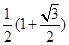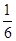＝×mv?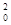
因为ΔE′＝f·x（1分），
可解得射入第二钢板的深度x为：（2分）
子弹打木块系统能量损失完全转化为了热量，相互作用力乘以相对位移为产生的热量，以系统为研究对象由能量守恒列式求解

本题难度：一般

3、选择题  如图16-6所示，人站在小车上，不断用铁锤敲击小车的一端.下列各种说法哪些是正确的(?)

图16-6
①如果地面水平、坚硬光滑，则小车将在原地附近做往复运动?②如果地面的阻力较大，则小车有可能断断续续地水平向右运动?③因为敲打时，铁锤跟小车间的相互作用力属于内力，小车不可能发生运动?④小车能否运动，取决于小车跟铁锤的质量之比，跟其他因素无关
A．①②
B．只有①
C．只有③
D．只有④

参考答案：A

本题解析：如果地面水平且坚硬光滑，据铁锤下摆过程中系统水平方向动量守恒可以判断小车向左移动；敲击后铁锤弹起上摆时，小车向右运动，即小车做往复运动.如果地面的阻力足够大，小车可能不运动；如果阻力不太大，而铁锤打击力较大，致使小车受向右的合外力而断断续续地水平向右运动.

本题难度：简单

4、简答题  如图6-4-11所示，A、B是静止在水平地面上完全相同的两块长木板.A的左端和B的右端相接触.两板的质量皆为M="2.0" kg，长度皆为l="1.0" m.C是一质量为m="1.0" kg的小物块,现给它一初速度v0="2.0" m/s，使它从B板的左端开始向右滑动.已知地面是光滑的，而C与A、B之间的动摩擦因数皆为μ=0.10.求最后A、B、C各以多大的速度做匀速运动.取重力加速度g="10" m/s2.

图6-4-11

参考答案：0.563 m/s? 0.155 m/s? 0.563 m/s

本题解析：先假设小物块C在木板B上移动x距离后，停在B上，这时A、B、C三者的速度相等，设为v.由动量守恒得
mv0=（m+2M）v?①
在此过程中，木板B的位移为s，小木块C的位移为s+x.由功能关系得
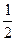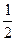-μmg（s+x）=mv2-mv02
μmgs=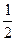·2Mv2
相加得-μmgx=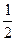（m+2M）v2-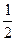mv02?②
解①②两式得x=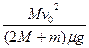
代入数值得x="1.6" m
x比B板的长度l大，这说明小物块C不会停在B板上，而要滑到A板上.设C刚滑到A板上的速度为v1，此时A、B板的速度为Ｖ1，则由动量守恒得mv0=mv1+2MＶ1
由功能关系得
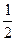mv0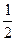2-mv12-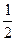·2MV12=μmgl
以题给数据代入解得V1=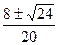?m/s
v1=2-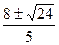?m/s=?m/s
由于v1必是正数，故合理的解是
V1=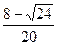?m/s="0.155" m/s? v1=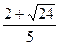?m/s=1.3８ m/s
当滑到A之后，B即以V1="0.155" m/s做匀速运动，而C以v1="1.38" m/s的初速在A上向右运动.设在A上移动了y距离后停止在A上，此时C和A的速度为v2，由动量守恒得
MV1+mv1=（m+M）v2
解得v2="0.563" m/s
由功能关系得
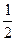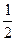mv12+MV12-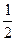（m+M）v22=μmgy
解得y="0.50" m
y比A板的长度小，故小物块C确实是停在A板上.最后A、B、C的速度分别为vA=v2="0.563" m/s，vB=v1="0.155" m/s，vC=vA="0.563" m/s.

本题难度：简单

5、填空题  如图所示，在验证动量守恒定律的实验中，将一个质量为m1的钢球A多次从斜槽轨道上端紧靠固定挡板处由静止释放，这个钢球经过斜槽轨道后由水平轨道飞出，在地面上落点的平均位置为P点．然后在水平轨道末端放置一个质量为m2的胶木球B（A、B两球的半径相等），将A球仍然多次从斜槽轨道的同一位置由静止释放，和球B发生碰撞，碰后两球分别落到地面上，根据两球落在地面的痕迹确定两球各自的落地点的平均位置分别为M点和N点．水平轨道末端重锤线指向地面的O点，测得OM=s1，OP=s2，ON=s3．重力加速度为g．
（1）若测量出水平轨道到地面的高度为h，则与B两球相碰前的瞬间A球的速度v1=______．
（2）在允许误差范围内，当m1、m2、s1、s2、s3满足关系式______时，就表明通过该实验验证了两球碰撞过程中动量守恒．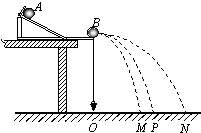

参考答案：（1）A球和B球相撞后，B球的速度增大，A球的速度减小，都做平抛运动，竖直高度相同，所以碰撞前A球的落地点是P点，
t=

本题解析：

本题难度：一般