微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、简答题 (1)如图6-15,在光滑水平长直轨道上,放着一个静止的弹簧振子,它由一轻弹簧两端各连接一个小球构成,两小球质量相等.现突然给左端小球一个向右的速度u0,求弹簧第一次恢复到自然长度时,每个小球的速度.
(2)如图6-16,将N个这样的振子放在该轨道上,最左边的振子1被压缩至弹簧为某一长度后锁定,静止在适当位置上,这时它的弹性势能为E0.其余各振子间都有一定的距离,现解除对振子1的锁定,任其自由运动,当它第一次恢复到自然长度时,刚好与振子2碰撞,此后,继续发生一系列碰撞,每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后,每个振子弹性势能的最大值.已知本题中两球发生碰撞时,速度交换,即一球碰后的速度等于另一球碰前的速度.
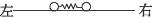
图6-15
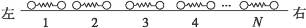
图6-16
参考答案:(1)u1=0,u2=u0? (2)EN=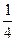 E0
E0
本题解析:(1)设每个小球质量为m,以u1、u2分别表示弹簧恢复到自然长度时左右两端小球的速度,由动量守恒和能量守恒定律有
mu1+mu2=mu0(以向右为速度正方向)
 mu12+
mu12+ mu22=
mu22= mu02
mu02
解得u1=u0,u2=0或u1=0,u2=u0
由于振子从初始状态到弹簧恢复到自然长度的过程中,弹簧一直是压缩状态,弹力使左端小球持续减速,使右端小球持续加速,因此应该取解析u1=0,u2=u0.
(2)以v1、v1′分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度,规定向右为速度的正方向,由动量守恒和能量守恒定律
mv1+mv1′=0
 mv12+
mv12+ mv1′2=E0
mv1′2=E0
解得v1=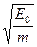 ,v1′=-
,v1′=-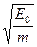 或v1=-
或v1=-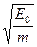 ,v1′=
,v1′=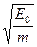 .
.
在这一过程中,弹簧一直是压缩状态,弹性力使左端小球向左加速,右端小球向右加速,故应取解析
v1=-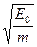 ,v1′=
,v1′=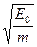
振子1与振子2碰撞后,由于交换速度,振子1右端小球速度变为0,左端小球速度仍为v1.此后两小球都向左运动,当它们向左的速度相同时,弹簧被拉伸至最长,弹性势能最大,设此速度为v10,根据动量守恒定律:
2mv10=mv1
用E1表示最大弹性势能,由能量守恒有
 mv102+
mv102+ mv102+E1=
mv102+E1= mv12
mv12
解得E1=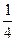 E0
E0
振子2被碰撞后瞬间,左端小球速度为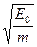 ,右端小球速度为0.以后弹簧被压缩,当弹簧再恢复到自然长度时,根据(1)题结果,左端小球速度v2=0,右端小球速度v2′=
,右端小球速度为0.以后弹簧被压缩,当弹簧再恢复到自然长度时,根据(1)题结果,左端小球速度v2=0,右端小球速度v2′=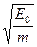 ,与振子3碰撞,由于交换速度,振子2右端小球速度变为0,振子2静止,弹簧为自然长度,弹性势能为E2=0.
,与振子3碰撞,由于交换速度,振子2右端小球速度变为0,振子2静止,弹簧为自然长度,弹性势能为E2=0.
同样分析可得
E2=E3=…=EN-1=0
振子N被碰撞后瞬间,左端小球速度vN-1′=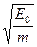 ,右端小球速度为0,弹簧处于自然长度.此后两小球都向右运动,弹簧被压缩,当它们向右的速度相同时,弹簧被压缩至最短,弹性势能最大.设此速度为vN0,根据动量守恒定律,
,右端小球速度为0,弹簧处于自然长度.此后两小球都向右运动,弹簧被压缩,当它们向右的速度相同时,弹簧被压缩至最短,弹性势能最大.设此速度为vN0,根据动量守恒定律,
2mvN0=mvN-1′
用EN表示最大弹性势能,根据能量守恒,有
 mvN02+
mvN02+ mvN02+EN=
mvN02+EN= mvN-12
mvN-12
解得EN=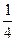 E0.
E0.
本题难度:简单
2、简答题 如图17-1所示,A、B是静止在水平地面上完全相同的两块长木板.A的左端和B的右端相接触.两板的质量皆为M=2.0kg,

长度皆为L=1.0m.C是质量为m=1.0kg的小物块.现给它一初速度v0=2.0m/s,使它从板B的左端向右滑动.已知地面是光滑的,而C与板A、B之间的动摩擦因数皆为μ=0.10.求最后A、B、C各以多大的速度做匀速运动.取重力加速度g=10m/s2.
参考答案:A、B、C的速度分别为vA=v3=0.563m/s,vB=v2=0.155m/s,vC=vA=0.563m/s.
本题解析:先假设小物块C在木板B上移动x距离后,停在B上.这时A、B、C三者的速度相等,设为v,由动量守恒得
mv0=(m+2M)v, ①
在此过程中,木板B的位移为s,小物块C的位移为s+x.由功能关系得
-μmg(s+x)=(1/2)mv2-(1/2)mv02,
μmgs=2Mv2/2,
则 -μmgx=(1/2)(m+2M)v2-(1/2)mv02,②
由①、②式,得
x=[mv02/(2M+m)μg], ③
代入数值得 x=1.6m. ④
x比B板的长度大.这说明小物块C不会停在B板上,而要滑到A板上.设C刚滑到A板上的速度为v1,此时A、B板的速度为v2,则由动量守恒得
mv0=mv1+2Mv2, ⑤
由功能关系,得(1/2)mv02-(1/2)mv12-2×(1/2)mv22=μmgL,
以题给数据代入,得


由v1必是正值,故合理的解是
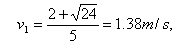
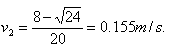
当滑到A之后,B即以v2=0.155m/s做匀速运动,而C是以v1=1.38m/s的初速在A上向右运动.设在A上移动了y距离后停止在A上,此时C和A的速度为v3,由动量守恒得
Mv2+mv1=(m+M)v3,
解得 v3=0.563m/s.
由功能关系得
(1/2)mv12+(1/2)mv22-(1/2)(m+M)v32=μmgy,
解得 y=0.50m.
y比A板的长度小,所以小物块C确实是停在A板上.最后A、B、C的速度分别为vA=v3=0.563m/s,vB=v2=0.155m/s,vC=vA=0.563m/s.
评分标准 本题的题型是常见的碰撞类型,考查的知识点涉及动量守恒定律与动能关系或动力学和运动学等重点知识的综合,能较好地考查学生对这些重点知识的掌握和灵活运动的熟练程度.题给数据的设置不够合理,使运算较复杂,影响了学生的得分.从评分标准中可以看出,论证占的分值超过本题分值的50%,足见对论证的重视.而大部分学生在解题时恰恰不注重这一点,平时解题时不规范,运算能力差等,都是本题失分的主要原因.
解法探析 本题参考答案中的解法较复杂,特别是论证部分,①、②两式之间的两个方程可以省略.下面给出两种较为简捷的论证和解题方法.
解法一 从动量守恒与功能关系直接论证求解.设C刚滑到A板上的速度为v1,此时A、B板的速度为v2,则由动量守恒,得?
mv0=mv1+2Mv2,
以系统为对象,由功能关系,得
1/2)mv02-(1/2)mv12-2×(1/2)mv22=μmgL,
由于v1只能取正值,以题给数据代入得到合理的解为
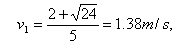
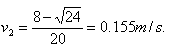
由于小物块C的速度v1大于A、B板的速度v2,这说明小物块C不会停在B板上.
以上过程既是解题的必要部分,又作了论证,比参考答案中的解法简捷.后面部分与参考答案相同,不再缀述.
解法二 从相对运动论证,用动量守恒与功能关系求解.
以地面为参照系,小物块C在A、B上运动的加速度为aC=μg=1m/s2,A、B整体的加速度为aAB=μmg/2M=0.25m/s2,C相对A、B的加速度a=aC+aAB=1.25m/s2.假设A、B一体运动,以A、B整体为参照物,当C滑至与整体相对静止时,根据运动学公式,有
v02=2as,
解得 s=v02/2a=1.6m>L.
说明小物块C不会停在B板上.
本题难度:简单
3、计算题 如图所示。光滑水平面上的木板C的质量mC=2kg、长l=2m,它的BA两端各有块挡板。木板的正中央并列放着两个可以视为质点的滑块A和B,它们的质量mA=1kg、mB=4kg,A、B之间夹有少许炸药。引爆炸药,A、B沿同一直线向两侧分开,运动到两端的挡板时与板粘贴在一起。A、B与木板C之间的摩擦不计。引爆时间及A、B跟挡板碰撞的时间也不计。若爆炸后A获得的速度vA=6m/s,试计算:
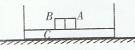
小题1:A、B都与挡板粘贴在一起以后,木板C的速度。
小题2:从引爆炸药到A、B 都与挡板粘贴在一起的时间差。
参考答案:
小题1:0
小题2:0.214s
本题解析:

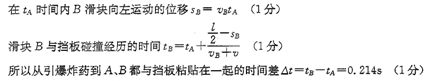
本题难度:简单
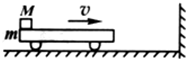
4、简答题 如图所示,水平平板小车质量为m=2kg,其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求:
①欲使M不从小车上落下,小车至少多长?
②第一次反弹后到最终状态,小车运动的总路程.(小车与水平面的摩擦不计,g=10m/s2)
参考答案:①取平板车与铁块为研究系统,由M>m,系统每次与墙碰后m反向时,M仍以原来速度向右运动,系统总动量向右,故会多次反复与墙碰撞,每次碰后M都要相对m向右运动,直到二者停在墙边,碰撞不损失机械能,系统的动能全在M相对m滑动时转化为内能.设M相对m滑动的距离为s,则有:
μMgs=12(m+M)v2
解得:s=(m+M)v22μMg=403m
欲便M不从小车上落下,则L≥s,故小车长为:L≥403m
②小车第一次反弹向左以10m/s的速度做减速运动,直到速度为零,其加速度大小为:a=μMgm=15m/s2
故小车第一次向左的最大位移为:s1=v022a
代入数据得:s1=103m
设小车第n-1次碰前速度为vn-1,第n次碰前速度为vn,则第n-1次碰后到第n次碰前过程动量守恒,有:Mvn-1-mvn-1=(m+M)vn,
所以有:vn=M-mM+mvn-1=12vn-1
第n-1次碰后小车反弹速度为vn-1,向左减速的最大位移为:sn-1=vn-122a
随后向右加速距离为:s′=vn22a
显然有:vn<vn-1,s′<sn-1
所以在碰前有相等速度,第n次碰后向左运动的最大位移为:
sn=vn22a
所以有:snsn-1=vn2vn-12=14,
即成等比数列.小车运动的总路程为:
s=2(s1+s2+s3+…+sn…)=2s11-snsn-1=2×1031-14=809m
答:①欲使M不从小车上落下,小车至少403m.
②第一次反弹后到最终状态,小车运动的总路程809m.
本题解析:
本题难度:一般
5、简答题 如图16-3-8所示,在质量均为m的A、B两球之间,用轻弹簧将它们连着,然后放于光滑的水平面上.如果A球被水平射来的速度为v0的子弹击中,并嵌入球中,且子弹质量为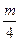 ,问在以后的运动过程中:
,问在以后的运动过程中:
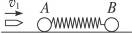
图16-3-8
(1)弹簧的弹性势能的最大值为多少?
(2)B球的最大动能为多少?
参考答案:(1)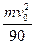 ? (2)
? (2)
本题解析:(1)子弹击中A的瞬间,子弹和A组成的系统动量守恒,B的瞬时速度为零.
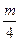 v0=(m+
v0=(m+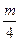 )vA,得vA=
)vA,得vA=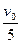 .
.
当A、B和子弹有共同速度时,弹性势能最大.
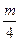 v0=(m+m+
v0=(m+m+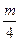 )v,v=
)v,v=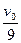 ,所以最大弹性势能为
,所以最大弹性势能为
Ep= (m+
(m+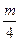 )vA2-
)vA2- ?(m+m+
?(m+m+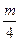 )v2=
)v2=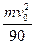 .
.
(2)当弹簧恢复原长时,B的动能最大
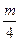 v0=(m+
v0=(m+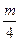 )vA′+mvB
)vA′+mvB
 ?(m+
?(m+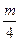 )vA2=
)vA2= ?(m+
?(m+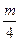 )vA′2+
)vA′2+ mvB2
mvB2
得EkB= mvB2=
mvB2= .
.
本题难度:简单