微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 一电子在匀强磁场中,以一固定的正电荷为圆心,在圆形轨道上运动,磁场方向垂直于它的运动平面,电场力恰是磁场力的三倍.设电子电量为e,质量为m,磁感强度为B,那么电子运动的可能角速度应当是 (? )
A.
B.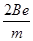
C.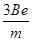
D.
参考答案:BD
本题解析:由于不知道磁场方向和电荷运动方向,但是知道洛伦兹力和速度垂直,因此分洛伦兹力指向圆心和背离圆心两种情况进行分析,然后根据向心力公式列方程即可求解.
当洛伦兹力方向和电场力方向相同时,有
其中: ,联立解得
,联立解得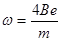
当洛伦兹力方向和电场力方向相反时,有: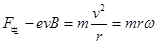
其中: ,联立解得
,联立解得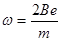
所以BD正确,
点评:此类型的题目关键是熟练运用向心力公式的各种表达式正确解答.
本题难度:一般
2、计算题 在水平地面上方足够大的真空室内存在着匀强电场和匀强磁场共存的区域,电场与磁场的方向始终平行。在距离水平地面某一高度处,有一个带电量为-q、质量为m的带电质点,以垂直于电场方向的水平初速度v0进入该真空室内,取重力加速度为g。求:
(1)要使带电质点进入真空室后做半径为R的匀速圆周运动,求磁感应强度B0的大小及所有可能的方向;
(2)当磁感应强度的大小变为B时,为保证带电质点进入真空室后做匀速直线运动,求此时电场强度E的大小和方向应满足的条件;
(3)在满足第(2)问的条件下,当带电质点运动到空中某一位置M点时立即撤去磁场,之后质点运动到空中另一位置N点时的速度大小为v,求M、N两点间的竖直高度H及经过N点时重力做功的功率。
参考答案:解:(1)带电质点在匀强电场E0和匀强磁场B0共存的区域做匀速圆周运动,电场力必定与重力平衡,即:qE0=mg
由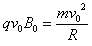 ,解得:
,解得: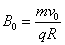
磁感应强度B0方向为竖直向上或竖直向下
(2)磁场B和电场E方向相同时,如图甲所示;磁场B和电场E方向相反时,如图乙所示。带电质点做匀速直线运动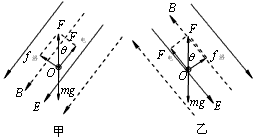 所以
所以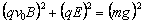
解得: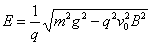
电场E的方向为沿与重力方向夹角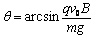 ,且斜向下的一切方向
,且斜向下的一切方向
或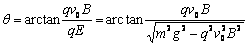 ,且斜向下方的一切方向
,且斜向下方的一切方向
(3)当撤去磁场后,带电质点所受电场力和重力的合力大小为qv0B,方向既垂直初速度v0的方向也垂直电场E的方向
设空中M、N两点间的竖直高度为H,因电场力不做功,机械能守恒定律
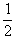 mv02+mgH=
mv02+mgH=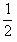 mv2,解得
mv2,解得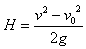
带电质点做类平抛运动,质点到达N点时沿合力方向的分速度大小为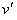 =
=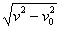
在这个过程中电场力不做功,重力的功率等于合外力在此时的瞬时功率
P=qv0B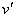 =
=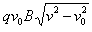
本题解析:
本题难度:困难
3、简答题 如图所示,虚线上方有场强为E1=6×104N/C的匀强电场,方向竖直向上,虚线下方有场强为E2的匀强电场,电场线用实线表示,另外,在虚线上、下方均有匀强磁场,磁感应强度相等,方向垂直纸面向里,ab是一长为L=0.3m的绝缘细杆,沿E1电场线方向放置在虚线上方的电、磁场中,b端在虚线上,将一套在ab杆上的带电量为q=-5×10-8C的带电小环从a端由静止释放后,小环先作加速运动而后作匀速运动到达b端,小环与杆间的动摩擦因数μ=0.25,不计小环的重力,小环脱离ab杆后在虚线下方仍沿原方向作匀速直线运动.
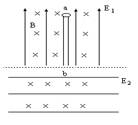
(1)请指明匀强电场E2的场强方向,说明理由,并计算出场强E2的大小;
(2)若撤去虚线下方电场E2,其他条件不变,小环进入虚线下方区域后运动轨迹是半径为L/3的半圆,小环从a到b的运动过程中克服摩擦力做的功为多少?
?
参考答案:(1)电场方向向左,2.4×105N/C
(2)-3×10-4J
本题解析:设匀强磁场的磁感应强度为B,带电粒子在虚线上方匀速运动速度为V,
(1)带电小环在虚线上方做匀速运动时,有
μBvq=qE1 (1)
带电小环在虚线下方做匀速运动,洛仑兹力的方向向左,由于小环做匀速运动,可知电场力方向应向右,电场方向向左
Bvq=qE2 (2)
解(1)、(2)得,E2=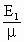 =
= N/C=2.4×105N/C
N/C=2.4×105N/C
(2)若去掉虚线下方的电场后,带电小环做圆围运动,有
? Bvq=m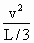 (3)
(3)
得?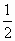 mV2=
mV2=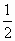 ×
×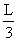 ×Bvq=
×Bvq=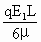
在虚线上方,电场力做功 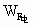 =qE1L
=qE1L
根据动能定理 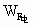 +Wf=
+Wf=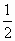 mV2-0
mV2-0
? Wf=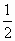 mV2-
mV2- =
=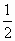 mV2-qE1L=
mV2-qE1L=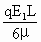 -qE1L
-qE1L
=(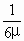 -1)qE1L=(
-1)qE1L=(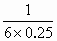 -1)×6×104×5×10-8×0.3J
-1)×6×104×5×10-8×0.3J
=-3×10-4J
本题难度:一般
4、选择题 如图所示,一束正离子 从S点沿水平方向射出,在没有偏转电场、磁场时恰好击中荧光屏上的坐标原点O;若同时加上电场和磁场后,正离子束最后打在荧光屏上坐标系的第Ⅲ象限中,则所加电场E和磁场B的方向可能是(不计离子
从S点沿水平方向射出,在没有偏转电场、磁场时恰好击中荧光屏上的坐标原点O;若同时加上电场和磁场后,正离子束最后打在荧光屏上坐标系的第Ⅲ象限中,则所加电场E和磁场B的方向可能是(不计离子 重力及其之间相互作用力)
重力及其之间相互作用力)
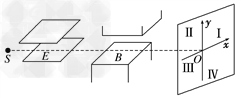
[? ]
A.E向下,B向上?
B.E向下,B向下
C.E向上,B向下?
D.E向上,B向上
参考答案:A
本题解析:
本题难度:一般
5、计算题 如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场。在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E。一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力。
(1)求磁感应强度B的大小;
(2)若粒子以速度v从O点垂直于磁场方向射入第一象限,当速度方向沿x轴正方向的夹角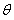 =30°时,求粒子从射入磁场到最终离开磁场的时间t。
=30°时,求粒子从射入磁场到最终离开磁场的时间t。

参考答案:解:(1)设粒子在磁场中做圆运动的轨迹半径为R,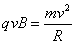
粒子自A点射出,由几何知识,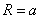
解得
(2)粒子在磁场中做圆运动的周期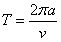
粒子从磁场中的P点射出,因磁场圆和粒子的轨迹圆的半径相等,OO1PO2构成菱形,故粒子从P点的出射方向与y轴平行,粒子由O到P所对应的圆心角为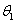 =60°
=60°
由几何知识可知,粒子由P点到x轴的距离S=acos
粒子在电场中做匀变速运动,在电场中运动的时间
粒子由P点第2次进入磁场,由Q点射出,PO1QO3构成菱形,由几何知识可知Q点在x轴上,粒子由P到Q的偏向角为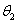 =120°,则
=120°,则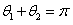
粒子先后在磁场中运动的总时间
粒子在场区之间做匀速运动的时间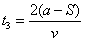
解得粒子从射入磁场到最终离开磁场的时间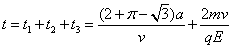

本题解析:
本题难度:困难