1、简答题  一个小球在水平面上做匀速直线运动，经5s前进1.2m，来到一个下坡路做匀加速直线运动，坡长3m，到达坡底是速度为1.26m/s．求小球在斜坡上运动的加速度以及小球在斜坡上的运动时间．

参考答案：小球在斜坡上的初速度为在水平面上匀速运动的速度，即
v0=xt=1.25m/s=0.24m/s
在斜坡上做匀加速直线运动，根据速度与位移的关系公式v2-v02=2ax，得
a=v2-v022x=1.262-0.2422×3m=0.255m/s2
根据匀变速运动的平均速度公式x=v0+v2t得
t=2xv0+v=2×30.24+1.26s=4s
答：小球在斜坡上运动的加速度为0.255m/s2，小球在斜坡上的运动时间为4s．

本题解析：

本题难度：一般

2、实验题  在做“研究匀变速直线运动”的实验时,某同学得到一条用打点计时器打下的纸带,并在其上取了A、B、C、D、E、F等6个计数点(每相邻两个计数点间还有4个打点计时器打下的点,本图中没有画出)打点计时器接的是220V、50Hz的交变电流.他把一把毫米刻度尺放在纸带上,其零刻度和计数点A对齐.(下述第(1)、(2)、(3)小题结果均保留两位有效数字)

(1)由以数据计算打点计时器在打C点时,物体的瞬时速度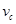是______ ;
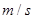(2)计算该物体的加速度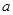为________ ;
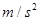(3)纸带上的A点所对应的物体的瞬时速度="______" ;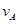
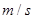(4)如果当时电网中交变电流的频率是,而做实验的同学并不知道,那么由此引起的系统误差将使加速度的测量值比实际值偏_______(填“大”或“小”).

参考答案：(1)0.16—0.17；(2) 0.40—0.45；(3) 0.070—0.080；（4）大

本题解析：
试题分析:（1）每相邻两个计数点间还有4个打点计时器打下的点，即相邻两个计数点的时间间隔是T=0.1s，根据匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，有：vC=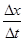==0.16m/s；
（2）据运动学公式采用逐差法求解加速度，根据公式△x=aT2，有CE-AC=4aT2，得a=0.42m/s2；
（3）由匀变速直线运动速度与时间关系式得：vA=vC-a(2T)=0.076m/s。
（4）当时电网中交变电流的频率是时，相邻两个计数点的时间间隔是T变大了，但做实验的同学并不知道，用了较小的T，所以引起的系统误差将使加速度的测量值比实际值偏“大”.

本题难度：一般

3、计算题  （１４分）甲、乙两物体，甲的质量为１ｋｇ，乙的质量为０．５ｋｇ，甲从距地４５ｍ高处自由落下，１ｓ后乙从距地３０ｍ高处自由落下，不计空气阻力．（重力加速度ｇ取１０）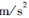
（１）两物体等高时离地多高？
（２）定量画出两物体间的竖直距离随时间变化的图象．（球落地后立即原地静止，规定甲开始下落时刻为计时起点．）

参考答案：（1）25m；（2）图像如下图所示。

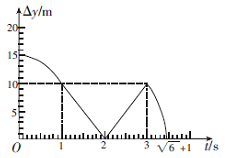
本题解析：（1）两物体的加速度均为g，方向竖直向下，设甲下落时间t时二者相遇，
则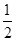gt2=15+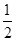g(t－1)2，解得t=2s
此时两物体离地高度H=45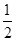－gt2=25m
（2）以甲下落的初位置 91ExaM.org为坐标原点，下落时刻为计时起点，竖直向下为正方向，设时间t甲、乙的位置坐标分别为y1、y2，则0～1s内两物体的竖直距离随时间的关系为
△y1=15－y1=15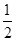－gt2=15－5t2
1～2s内两物体的竖直距离随时间的关系为
△y2=y2－y1=[15+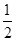g(t－1)2]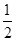－gt2=20－10t
设经过t时间落地，则45=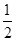gT2，解得T=3s
设乙在空中运动时间为T′，则有0=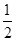gT′2，解得T′=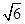s
2～3s内两物体的竖直距离随时间的关系为
△y3=y1－y2=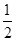gt2－[15+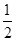g(t－1)2]=10t－20
3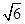～（+1）s内两物体的竖直距离随时间的关系为
△y4=45－y2=45－[15+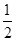g(t－1)2]=25+10t－5t2
则图象如上所示（每段2分）

本题难度：一般

4、计算题  （8分）某型号的舰载飞机在航空母舰的跑道上加速时，发动产生的最大加速度为5ｍ/ｓ2，所需的起飞速度为50ｍ/ｓ，跑道长100ｍ，通过计算判断，飞机能不能靠自身的发动机从舰上起飞？为了飞机在开始滑行时就有一定的初速度，航空母舰装有弹射装置，对于该型号的舰载飞机，弹射系统必须使它具有多大的初速度？为了尽量缩短舰载飞机起飞时滑行的距离，航空母舰还需逆风行驶，这里对问题做了简化。

参考答案：不能? v 0＝39m／s

本题解析：若飞机靠自身发动机起飞，飞机初速度为0，加速度a＝5m／s2，位移x＝100m，
末速度为v。
由v2-v02=2ax得v<50m/s，所以不能。
弹射装置使飞机初速度为v0，末速度为v＝50m／s
根据v 2- v 02＝2ax?解得：v 0＝39m／s　
点评：本题学生要能灵活应用推论公式v2-v02=2ax解相关问题。

本题难度：简单

5、简答题  如图所示，一质量为M=5.0kg的平板车静止在光滑水平地面上，平板车的上表面距离地面高为h，其右侧足够远处有一障碍物A，另一质量为m=2.0kg可视为质点的滑块，以v0=8m/s的初速度从左端滑上平板车，同时对平板车施加一水平向右、大小为5N的恒力F，当滑块运动到平板车的最右端时，二者恰好相对静止，此时撤去恒力F，当平板车碰到障碍物A时立即停止运动，滑块水平飞离平板车后，恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道，并沿轨道下滑，已知滑块与平板车间的动摩擦因数μ=0.5，圆弧半径为R=2m，圆弧所对的圆心角∠BOD=θ=106°，取g=10m/s2，sin53°=0.8，cos53°=0.6，求：（1）平板车的长度；（2）障碍物A与圆弧左端B的水平距离．（3）滑块在C点处对轨道的压力大小是多少？

参考答案：（1）对滑块，由牛顿第二定律得a1=μmgm=μg=5m/s2
对平板车，由牛顿第二定律得?a2=F+μmgM=3m/s2
设经过时间t1，滑块与平板车相对静止，共同速度为υ，
则υ=υ0-a1t1=a2t1
解得?t1=1s?
υ=3m/s
滑块与平板车在时间t1内通过的位移分别为?
x1=υ0+υ2t1，
x2=υ2t1
则平板车的长度为?L=x1-x2=υ02t1=4m．?
（2）设滑块从平板车上滑出后做平抛运动的时间为t2，因滑块恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道，
对B处速度进行分解可知：
tan53°=υyυx?
?又υx=υ=3m/s?
得υy=4m/s?
由公式υy=gt2xAB=υxt2
解得xAB=1.2m?
（3）在B点的速度的大小为 υB=

本题解析：

本题难度：一般