1、计算题  分）如图所示，空间存在着强度E=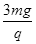方向竖直向上的匀强电场，在电场内一长为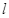的绝缘细线，一端固定在O点，一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求：

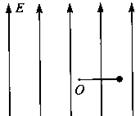
（1）小球运动最高点时的速度；
（2）细线能承受的最大拉力；
（3）从断线开始计时，在t=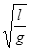时刻小球与O点的距离。

参考答案：（1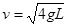）；（2）6mg；（3）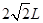

本题解析：
试题分析:
（1）设小球运动到最高点时速度为v，只有重力和电场力做功，弹力不做功。对该过程由动能定理有，
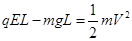?①?（2分）
解得?（1分）
（2）在最高点，小球受三个力作用，重力，电场力和细线的拉力，由向心力公式得，
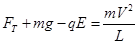?②（2分）
解得，T=6mg（1分）
（2）小球在细线断裂后，带电小球做类平抛运动，合力竖直向上的，在竖直方向的加速度设为a，则
?③（2分）
小球在t时刻
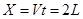?（1分）
?（1分）
小球与O点的距离
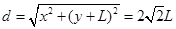? (2分）

本题难度：一般

2、选择题  质量为m的物体，从静止出发以

参考答案：根据牛顿第二定律得，物体的合力F合=ma=12mg，则合力做功为W合=F合h=12mgh，所以动能的增加量为12mgh．物体上升h，则重力势能的增加量为mgh，机械能等于动能和重力势能之和，所以机械能增加32mgh．故A、B、D正确，C错误．
故选：ABD．

本题解析：

本题难度：简单

3、简答题  如图所示为研究某种弹射装置的示意图，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带足够长，皮带轮沿逆时针方向转动，带动皮带以恒定速度v=2.0m/s匀速传动．三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上，开始时在B、C间有一压缩的轻弹簧，两滑块用细绳相连处于静止状态．滑块A以初速度v0=4.0m/s沿B、C连线方向向B运动，A与B碰撞后粘合在一起，碰撞时间极短，可认为A与B碰撞过程中滑块C的速度仍为零．因碰撞使连接B、C的细绳受扰动而突然断开，弹簧伸展，从而使C与A、B分离．滑块C脱离弹簧后以速度vC=4.0m/s滑上传送带．已知滑块C与传送带间的动摩擦因数μ=0.20，重力加速度g取10m/s2．

（1）求滑块C在传送带上向右滑动距N点的最远距离sm；
（2）求弹簧锁定时的弹性势能Ep；
（3）求滑块C在传送带上运动的整个过程中与传送带之间因摩擦产生的内能Q．

参考答案：（1）滑块C滑上传送带做匀减速运动，当速度减为零时，滑动的距离最远．
由动能定理?-μmgsm=0-12mv2C
解得sm=4.0?m
（2）设A、B碰撞后的速度为v1，A、B与C分离时的速度为v2，由动量守恒定律
mv0=2mv1
2mv1=2mv2+mvC
解得v1=12v0，v2=0
由能量守恒定律
Ep+12×2mv12=12×2mv22+12mvC2
解得Ep=4.0?J
（3）滑块在传送带上向右匀减速运动，设滑块C在传送带上运动的加速度为a，滑块速度减为零的时间为t1，向右的位移为s1，在同样时间内传送带向左的位移为x1，根据牛顿第二定律和运动学公式
a=μmgm=2m/s2．
滑块C速度减小到零所需的时间t1=vca=2s．
滑块的位移s1=vc22a=164m=4m．
传送带的位移x1=vt1=2×2m=4m，
相对路程△x1=s1+x1=8m．
然后滑块返回做匀加速直线运动，当速度达到传送带速度一起做匀速直线运动．
匀加速直线运动的时间t2=va=22s=1s，
滑块C的位移s2=12at22=12×2×1m=1m．
传送带的位移x2=vt2=2m
相对路程△x2=x2-s2=1m．
则摩擦产生的内能Q=μmg（△x1+△x2）=0.2×10×9J=18J．
答：（1）滑块C在传送带上向右滑动距N点的最远距离为4.0m．
（2）弹簧锁定时的弹性势能为4.0J．
（3）滑块C在传送带上运动的整个过程中与传送带之间因摩擦产生的内能为4.0J．

本题解析：

本题难度：一般

4、选择题  将质量为M=3m的木块固定在光滑水平面上，一颗质量为m的子弹以速度v0沿水平方向射入木块，子弹射穿木块时的速度为

参考答案：当木块固定时，根据动能定理得，-fd=12m(v03)2-12mv02，解得fd=49mv02．
当木块不固定，假设子弹不能射出木块，根据动量守恒定律得，mv0=（M+m）v，解得v=v04
根据能量守恒定律得，f△x=12mv02-12(M+m)v2=38mv02＜fd，可知△x＜d，所以假设成立，子弹不能射出木块，最终子弹和木块以相同的速度做匀速运动．故A正确，B、C、D错误．
故选A．

本题解析：

本题难度：简单

5、计算题  （18分）如图所示，现有一个小物块，质量为m=80g，带上正电荷q =2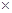10－4C。与水平的轨道之间的滑动摩擦系数m= 0.2，在一个水平向左的匀强电场中，E = 4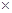103V/m，在水平轨道的末端N处，连接一个光滑的的半圆形轨道，半径为R=40cm，取g = 10m/s2，求：

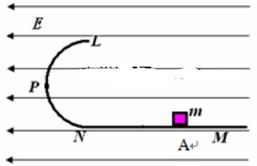
（1）若小物块恰能运动到轨道的最高点L，那么小物块应从距N点多远处的A点释放？
（2）如果小物块在上小题中的位置A释放，当它运动到P点（轨道中点）时轨道对它的支持力等于多少？
（3）小物块在位置A释放，当运动到N点时，突然撤去电场，同时加一匀强磁场，磁感应强度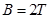，方向垂直纸面向里，问能否运动到L点？（回答：“能”或“不能”即可）如果小物块最后能落回到水平面MN上，则刚到达MN时小物块的速度大小为多少？

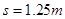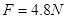参考答案：（1）（2）（3）能?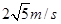

本题解析：（1）物块能通过轨道最高点L的条件是
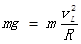?（2分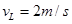）??（1分）
A到L过程根据动能定理有： ?（2分）
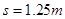解得??（1分）
（2）物块由P到L过程根据动能定理有：
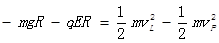?（2分）
VP=2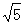m/s?（1分）
P点水平方向的支持力和电场力的合力提供向心力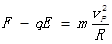：?（2分）
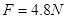?（1分）
（3）去电场，加磁场后，洛伦兹力与速度垂直，垂直圆弧面向外，而且到达N点的速度与之前相同，所有能到达L点?（3分）
小物块从N点运动到最高点再落回到MN水平面时过程，外力没有做功，所以速度的大小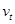等于第一次经过N点时的速度大小。
由动能定理:
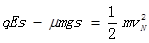?（2分）（或考虑物块N由L到过程,解答也可）
vt==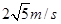?（1分）

本题难度：一般