微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、填空题 一高度为h的光滑弧形轨道固定在水平面上,如图所示.质量为m的物体A从轨道顶端由静止开始下滑到底面时速度的大小为______,此过程中重力对物体A做功为______.(空气阻力不计)
参考答案:根据动能定理得,mgh=12mv2-0,解得v=
本题解析:
本题难度:简单
2、选择题 加速上升的电梯顶部悬有一轻质弹簧,弹簧下端挂有一铁块,若电梯突然停止,以电梯底板为参考系,铁块在继续上升的过程中(?)
A.动能先增大后减小
B.动能逐渐减小
C.加速度逐渐增大
D.加速度不变
参考答案:A
本题解析:分析:电梯加速过程,铁块随电梯一起加速前进,拉力大于重力;电梯停止后,物体先加速上升,后减速上升,可以判断动能的变化情况和加速度的变化情况.
解答:解:A、B、电梯加速过程,铁块随电梯一起加上升,受拉力F和重力G
F-G=ma
故F>G
电梯突然停止后,铁块由于惯性继续上升,先加速,当拉力减小到等于重力时加速度减为零,速度达到最大,之后铁块由于惯性仍然继续上升,弹力开始小于重力,物体做加速度不断增大的减速运动,又由于动能Ek= mv2,因而A正确,B错误;
mv2,因而A正确,B错误;
C、D、由上述分析可知,物体先做加速度不断减小的加速运动,后作加速度不断增大的减速运动,因而CD均错误;
故选A.
本题难度:一般
3、计算题 如图,质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计。设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中。开始时,杆OB与竖直方向的夹角θ0=60°,由静止释放,摆动到θ=90°的位置时,系统处于平衡状态,求:
(1)匀强电场的场强大小E;
(2)系统由初位置运动到平衡位置,重力做的功Wg和静电力做的功We;
(3)B球在摆动到平衡位置时速度的大小v。

参考答案:解:(1)力矩平衡时:(mg-qE)lsin90°=(mg+qE)lsin(120°-90°)
即mg-qE=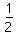 (mg+qE)
(mg+qE)
E=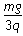
(2)重力做功:Wg=mgl(cos30°-cos60°)-mglcos60°=(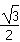 -1)mgl
-1)mgl
静电力做功:We=qEl(cos30°-cos60°)+qElcos60°=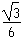 mgl
mgl
(3)小球动能改变量△Ek=Wg+We=( -1)mgl
-1)mgl
小球的速度v= =
=
本题解析:
本题难度:困难
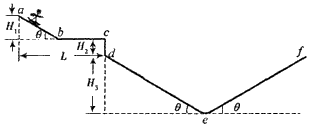
4、计算题 滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性。如图所示,abcdef为同一竖直平面内的滑行轨道,其中bc段水平,ab、de和ef段均为倾角37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略)。已知H1=5m,L=15m,H2=1.25m,H3=12.75m,设滑板与轨道之间的摩擦力为它们间压力的k倍(k=0.25),运动员连同滑板的总质量m=60 kg。运动员从a点由静止开始下滑从c点水平飞出,在de上着陆后,经短暂的缓冲动作后保留沿斜面方向的分速度下滑,接着在def轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取g=10 m/s2,sin37°=0.6,cos37°=0.8。求:
(1)运动员从c点水平飞出时的速度大小vc;
(2)运动员在de上着陆时,沿斜面方向的分速度大小v0;
(3)设运动员第一次和第四次滑上ef轨道时上升的最大高度分别为h1和h4,则h1:h4等于多少?
参考答案:解:(1)设运动员从a点到c点的过程中克服阻力做功Wf,根据动能定理
? 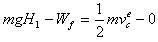 ?①?
?①?
?  ?②?
?②?
? 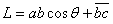 ?③
?③
? 由①②③式并代入数据,解得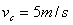 ④?
④?
(2)运动员从c点水平飞出到落到de轨道上的过程中做平抛运动,设从c点到着陆点经过的时间为t
? 水平位移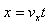 ⑤
⑤
? 竖直位移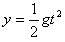 ⑥
⑥
? 由几何关系 ⑦
⑦
? 水平方向分速度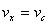 ⑧
⑧
? 竖直方向分速度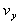
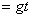 ⑨?
⑨?
?  ?⑩
?⑩
? 由④⑤⑥⑦⑧⑨⑩式并代入数据,解得 ?⑾
?⑾
(3)设运动员第一次沿ed斜面向上滑的最大高度为 ,根据功能关系
,根据功能关系
? 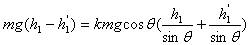 ?⑿
?⑿
? 解得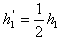 ⒀
⒀
? 同理可得,运动员第二次沿ef斜面向上滑的最大高度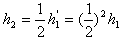 ⒁
⒁
? 以此类推,运动员第四次沿ef斜面向上滑的最大高度 ⒂
⒂
? 解得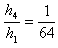
本题解析:
本题难度:困难
5、计算题 如图所示,四分之一圆轨道OA与水平轨道AB相切,它们与另一水平轨道CD在同一竖直面内,圆轨道OA的半径R=0.45m,水平轨道AB长s1=3m,OA与AB均光滑一滑块从O点由静止释放,当滑块经过A点时,静止在CD上的小车在F=1.6N的水平恒力作用下启动,运动一段时间后撤去力F,当小车在CD上运动了s2=3. 28m时速度v=24m/s,此时滑块恰好落入小车中,已知小车质量M=0.2kg,与CD间的动摩擦因数μ=0.4。(取g=10 m/s2)求
(1)恒力F的作用时间t。
(2)AB与CD的高度差h。

参考答案:解:(1)设小车在轨道CD上加速的距离为s,由动能定理得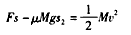 ①
①
设小车在轨道CD上做加速运动时的加速度为a,
由牛顿运动定律得F-μMg= Ma ②
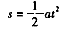 ③
③
联立①②③式,代入数据得 t=1s ④
(2)设小车在轨道CD上做加速运动的末速度为vˊ,撤去力F后小车做减速运动时的加速度为aˊ,
减速时间为tˊ,由牛顿运动定律得vˊ=at ⑤
-μMg= Maˊ⑥
v=v"十a"tˊ⑦
设滑块的质量为m,运动到A点的速度为vA,由动能定理得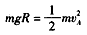 ⑧
⑧
设滑块由A点运动到B点的时间为t1,由运动学公式得s1=vAt1⑨
设滑块做平抛运动的时间为t1ˊ,则 f1ˊ=t+tˊ-t1 ⑩
联立②④⑤⑥⑦⑧⑨⑩ 式,代入数据得h=0.8m
式,代入数据得h=0.8m 。
。
本题解析:
本题难度:一般