微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 在电梯内的地板上,竖直放置一根轻质弹簧,弹簧上端固定一个质量为m的物体.当电梯静止时,弹簧被压缩了x;当电梯运动时,弹簧又被继续压缩了
.则电梯运动的情况可能是( )
A.以大小为g的加速度加速上升
B.以大小为g的加速度减速上升
C.以大小为g的加速度加速下降
D.以大小为g的加速度减速下降
参考答案:因为电梯静止时,弹簧被压缩了x,由此可以知道,
mg=kx,
当电梯运动时,弹簧又被继续压缩了x10,弹簧的弹力变大了,
所以物体的合力应该是向上的,大小是110mg,
由牛顿第二定律F=ma可得,
110mg=ma,
所以加速度大小为a=110g,
合力是向上的,当然加速度的方向也就是向上的,此时物体可能是向上的匀加速运动,也可能是向下的匀减速运动,所以D正确.
故选D.
本题解析:
本题难度:简单
2、选择题 甲、乙两位同学组成研究性学习小组,在运动着的一升降机内做“研究物体超重和失重现象”实验,站在磅秤上的甲同学发现了自已的体重增加了20%,重力加速度为g,于是乙同学对该过程中升降机的运动情况作出了如下判断,其中可能正确的是( )
A.升降机以0.2g的加速度加速下降
B.升降机以0.8g的加速度加速上升
C.升降机以0.2g的加速度减速下降
D.升降机以0.8g的加速度减速上升
参考答案:甲同学站在磅秤上受重力和支持力,发现了自已的体重增加了20%,
根据牛顿第二定律得出:a=FN-Gm=0.2g,该同学的加速度方向向上,
那么此时的运动可能是以0.2g的加速度减速下降,也可能是以0.2g的加速度加速上升,
故选C.
本题解析:
本题难度:一般
3、计算题 (12分)如图所示,AB为竖直半圆轨道的竖直直径,轨道半径R=0.9m,轨道B端与水平面相切,质量m=1kg的光滑小球从水平面以初速度V0向B滑动,取g=10m/s2。
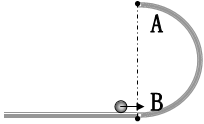
(1)若V0=6m/s,求小球经轨道最低点B瞬间对轨道的压力为多少?
(2)若小球刚好能经过A点,则小球在A点的速度至少为多大?小球离开A点后在水平面的落点与B点的距离为多少?
参考答案:见试题分析
本题解析:
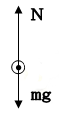
(1)小球在B点的受力分析如图:
由牛顿第二定律有: ?(公式2分)
?(公式2分)
解得小球受到的支持力N=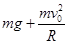 =50N?(答案1分)
=50N?(答案1分)
由牛顿第三定律可知,小球对道轨的压与与N大小相等,方向相反。?(1分)
(2)小球恰好过最高点,即只由重力提供向心力有:
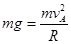 ?(2分)
?(2分)
解得小球在A点的最小速度: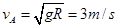 ?(1分)
?(1分)
小球离开A点后做平抛运动有: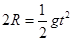 ?(2分)
?(2分)
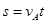 ?(2分)
?(2分)
解得t=0.6s? s=1.8m?(1分)
本题难度:一般
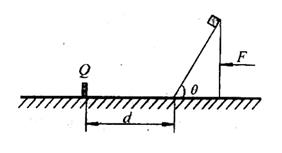
4、计算题 (14分)如图所示,在粗糙水平面上有一质量为M、高为h的斜面体,斜面体的左侧有一固定障碍物Q,斜面体的左端与障碍物的距离为d。将一质量为m的小物块置于斜面体的顶端,小物块恰好能在斜面体上与斜面体一起保持静止;现给斜面体施加一个水平向左的推力,使斜面体和小物块一起向左匀加速运动,当斜面体到达障碍物与其碰撞后,斜面体立即停止,小物块水平抛出,最后落在障碍物的左侧p处(图中未画出),已知斜面体与地面间的动摩擦因数为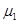 ,斜面倾角为
,斜面倾角为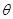 ,重力加速度为g,滑动摩擦力等于最大静摩擦力,求:
,重力加速度为g,滑动摩擦力等于最大静摩擦力,求:
(1)小物块与斜面间的动摩擦因数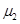 ;
;
(2)要使物块在地面上的落点p距障碍物Q最远,水平推力F为多大;
(3)小物块在地面上的落点p距障碍物Q的最远距离。
参考答案:见解析
本题解析:(1)物块恰好静止在斜面上: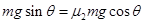
解得
(2)要使物块距P点最远,应使物块随斜面体到Q点的速度最大,需要加速度最大
对物块受力分析可得: ?①
?①
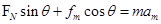 ?②
?②
 ? ③
? ③
由以上三式可解得 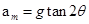
对整体列式: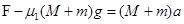
解得: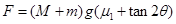
(3)物块抛出的速度
由平抛规律: ? x=vt
? x=vt
可解得: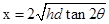
所以P距Q的距离为 。
。
本题难度:一般
5、计算题 如图所示,AB为半径R=0.8m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06 m,车上表面距地面的高度h=0.2m.现有一质量m=1kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5 s时,车被地面装置锁定.(g=10m/s2)试求:
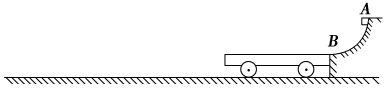
(1)滑块到达B端时,轨道对它支持力的大小;
(2)车被锁定时,车右端距轨道B端的距离;
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小;
(4)滑块落地点离车左端的水平距离.
参考答案:(1)30 N(2)1 m(3)6 J(4)0.16 m
本题解析:(1)设滑块到达B端时速度为v,
由动能定理,得mgR=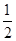 mv2
mv2
由牛顿第二定律,得FN-mg=m
联立两式,代入数值得轨道对滑块的支持力:FN=3mg=30 N.
(2)当滑块滑上小车后,由牛顿第二定律,得
对滑块有:-μmg=ma1
对小车有:μmg=Ma2
设经时间t两者达到共同速度,则有:v+a1t=a2t
解得t=1 s.由于1 s<1.5 s,此时小车还未被锁定,两者的共同速度:v′=a2t=1 m/s
因此,车被锁定时,车右端距轨道B端的距离:x=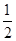 a2t2+v′t′=1 m.
a2t2+v′t′=1 m.
(3)从车开始运动到被锁定的过程中,滑块相对小车滑动的距离Δx=t-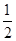 a2t2=2 m
a2t2=2 m
所以产生的内能:E=μmgΔx=6 J.
(4)对滑块由动能定理,得-μmg(L-Δx)=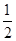 mv″2-
mv″2-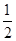 mv′2
mv′2
滑块脱离小车后,在竖直方向有:h=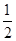 gt″2
gt″2
所以,滑块落地点离车左端的水平距离:x′=v″t″=0.16 m
点评:要根据牛顿第二定律和运动学公式,通过计算分析小车的状态,再求解车右端距轨道B端的距离,考查分析物体运动情况的能力.
本题难度:一般