微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,一束正离子垂直地射入正交的匀强磁场和匀强电场区域里,结果发现有些离子保持原来的运动方向未发生任何偏转.如果让这些不偏转的离子再垂直进入另一匀强磁场中,发现这些离子又分成几束.对这些进入后一磁场的不同轨迹的离子(不计重力),可得出结论:(?)
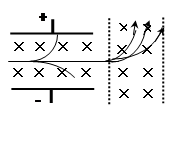
A.它们的荷质比一定各不相同
B.它们的电量一定各不相同
C.它们的速度大小一定相同
D.它们的质量一定各不相同
参考答案:AC
本题解析:粒子在磁场和电场正交区域里,同时受到洛伦兹力和电场力作用,粒子没有发生偏转,说明粒子所受电场力和洛伦兹力平衡,满足qvB=qE,即不发生偏转的粒子具有共同的速度大小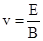 ,粒子进入磁场后受洛伦兹力作用做匀速圆周运动,满足
,粒子进入磁场后受洛伦兹力作用做匀速圆周运动,满足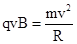 ,圆周运动的半径
,圆周运动的半径 ,由此进行分析得出结论.
,由此进行分析得出结论.
解:经过速度选择器后的粒子速度相同,粒子所受电场力和洛伦兹力平衡,满足qvB=qE,即不发生偏转的粒子具有共同的速度大小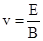 ;进入磁场区分开,轨道半径不等,根据公式
;进入磁场区分开,轨道半径不等,根据公式 ,只能说明比荷不同,故A正确,B错误,C正确,D错误。
,只能说明比荷不同,故A正确,B错误,C正确,D错误。
故选AC.
点评:能根据粒子不发生偏转得出粒子所受电场力和洛伦兹力平衡,并由此推算出粒子具有相同的速度v,在单独的匀强磁场中粒子分裂成几束说明粒子的荷质比不同,并由此得出电量、质量、以及速度所需要满足的关系式,从而得出正确的结论.
本题难度:一般
2、简答题 如图,在0≤x≤d的空间,存在垂直xOy平面的匀强磁场,方向垂直xOy平面向里.y轴上P点有一小孔,可以向y轴右侧垂直于磁场方向不断发射速率均为v、与y轴所成夹角θ可在0~1800范围内变化的带负电的粒子.已知θ=45°时,粒子恰好从磁场右边界与P点等高的Q点射出磁场,不计重力及粒子间的相互作用.求:
(1)磁场的磁感应强度;
(2)若θ=30°,粒子射出磁场时与磁场边界的夹角(可用三角函数、根式表示);
(3)能够从磁场右边界射出的粒子在磁场中经过的区域的面积(可用根式表示).
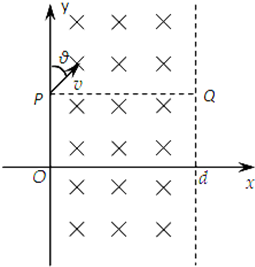
参考答案:(1)当θ=45°时,粒子恰好从磁场右边界与P点等高的Q点射出磁场,
由几何关系可得,d=Rcos45°
解得:R=
本题解析:
本题难度:一般
3、简答题 如图为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电量均不同的带电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域I的粒子质量m=6.4×10-27kg,带电量q=3.2×10-19C且d1=10cm,d2=5
cm,d3>10cm?E1=E2=40v/m,B1=4×10-3T,B2=×10-3T
求:能飞回区域Ⅰ的粒子第一次回到区域Ⅰ上边缘时离A的距离?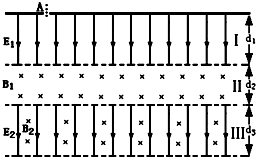
参考答案:
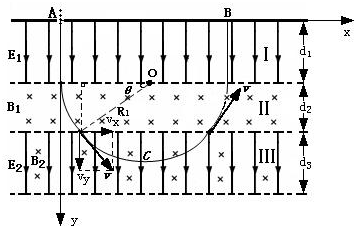
粒子在电场E1中做匀加速运动,由动能定理得
? qE1d1=12mv2
得:v=2×104m/s,方向竖直向下
粒子在磁场B1中偏转,则有:
qB1V=mv2R1
得:R1=0.1m
又sinθ=d2R1,得:θ=450
即粒子离开区域Ⅱ时的速度方向与X轴正向成45°角
粒子在E2与B2叠加场中:将速度V分解为Vx、Vy,则
? Vx=Vy=Vsin45°=
本题解析:
本题难度:一般
4、计算题 如图所示,在x<0与x >0的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向均垂直于纸面向里,且B1>B2。一个带负电荷的粒子从坐标原点O以速度V沿x轴负方向射出,要使该粒子经过一段时间后又经过O点,B1与B2的比值应满足什么条件?

?
?
?
?
参考答案: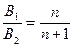 ?
?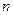 =1,2,
=1,2,
本题解析:粒子在整个过程中的速度大小恒为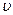 ,交替地在
,交替地在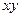 平面内
平面内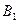 与
与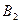 磁场区域中做匀速圆周运动,轨道都是半个圆周.设粒子的质量和电荷量的大小分别为
磁场区域中做匀速圆周运动,轨道都是半个圆周.设粒子的质量和电荷量的大小分别为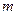 和
和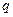 ,圆周运动的半径分别为
,圆周运动的半径分别为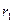 和
和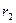 ,有
,有
得分得分 ?①?
?①?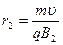 ?②
?②
现分析粒子运动的轨迹.如图所示,在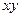 平面内,粒子先沿半径为
平面内,粒子先沿半径为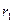 的半圆
的半圆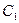 运动至
运动至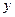 轴上离
轴上离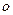 点距离为
点距离为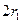 的
的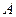 点,接着沿半径为
点,接着沿半径为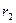 的半圆
的半圆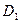 运动至
运动至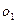 点,
点,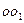 的距离
的距离 ?③
?③
此后,粒子每经历一次“回旋”(即从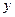 轴出发沿半径为
轴出发沿半径为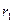 的半圆和半径为
的半圆和半径为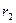 的半圆回到原点下方的
的半圆回到原点下方的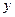 轴),粒子的
轴),粒子的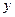 坐标就减小
坐标就减小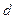 .设粒子经过
.设粒子经过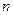 次回旋后与
次回旋后与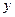 轴交于
轴交于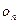 点,若
点,若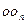 即
即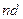 满足
满足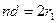 ?④则粒子再经过半圆
?④则粒子再经过半圆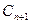 就能经过原点,式中
就能经过原点,式中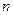 =1,2,3,……为回旋次数.由③④式解得
=1,2,3,……为回旋次数.由③④式解得
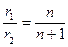 ?
?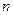 =1,2,3,……?⑤
=1,2,3,……?⑤
联立①②⑤式可得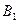 、
、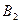 应满足的条件:
应满足的条件: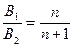 ?
?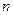 =1,2,
=1,2,
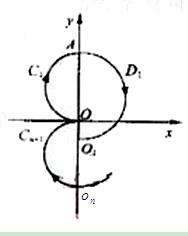
本题难度:简单
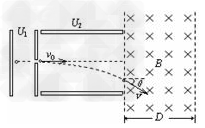
5、计算题 如图所示,一个质量为m =2.0×10-11 kg,电荷量q=+1.0×10-5 C的带电微粒(重力忽略不计),从静止开始经U1=100V电压加速后,水平进入两平行金属板间沿竖直方向的偏转电场中,偏转电场的电压U2=100V。金属板长L=20cm,两板间距d = cm。求:
cm。求:
(1)微粒进入偏转电场时的速度v0大小;
(2)微粒射出偏转电场时的偏转角θ;
(3)若该匀强磁场的宽度为D= cm,为使微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少多大。
cm,为使微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少多大。
参考答案:解:(1)微粒在加速电场中由动能定理得:qU1=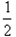 mv02? ①
mv02? ①
解得:v0=1.0×104m/s
(2)微粒在偏转电场中做类平抛运动,有: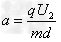 ;而
;而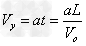
飞出电场时,速度偏转角的正切为:tanθ=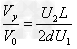 ②
②
解得θ=30°
(3)进入磁场时微粒的速度是:v=v0/cosθ?③
轨迹如图,由几何关系有: ?④?
?④?

洛伦兹力提供向心力:Bqv=mv2/r?⑤
由③~⑤联立得:B=mv0(1+sinθ)/qDcosθ
代入数据解得:B =0.4T?
所以,为使微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少为0.4T
本题解析:
本题难度:一般
Fair and softly to far in a day. 从容不慌,办事顺当.