1、计算题  中国探月卫星“嫦娥二号”升空后，首先进入周期为的近地圆轨道，然后在地面的指令下经过一系列的变轨后最终被月球捕获，经两次制动后在距离月球表面为的轨道上绕月球做匀速圆周运动． 已知地球质量为，半径为，月球质量为，半径为． 求：“嫦娥二号”绕月球运动时的周期（最终结果用题目中的物理量来表示）．

参考答案：解：“嫦娥二号”在近地空间运动时，有：?①
“嫦娥二号”绕月球运行时，有：?②
解得：?③

本题解析：略

本题难度：简单

2、填空题  设地球绕太阳做匀速圆周运动，半径为R，速率为v，则太阳的质量可用v、R和引力常量G表示为_______________，太阳围绕银河系中心的运动可视为匀速圆周运动，其运动速率约为地球公转速率的7倍，轨道半径约为地球公转轨道半径的2×l09倍，为了粗略估算银河系中恒星的数目，可认为银河系中所有恒星的质量都集中在银河系中心，且银河系中恒星的平均质量约等于太阳质量，则银河系中恒星数目约为 __________________。

参考答案：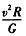

本题解析：

本题难度：一般

3、选择题  已知引力常数G和下列各组数据，能计算出地球质量的是（　　）
A．地球绕太阳运行的周期及地球离太阳的距离
B．月球绕地球运行的周期及月球离地球的距离
C．人造地球卫星在地面附近绕行的速度及运行周期
D．若不考虑地球自转，己知地球的半径及重力加速度

参考答案：A、地球绕太阳运动的周期和地球与太阳的距离，根据万有引力提供向心力：GMmr2=m?4π2rT2其中m为地球质量，在等式中消去，只能求出太阳的质量M．也就是说只能求出中心体的质量．故A错误．
B、月球绕地球做匀速圆周运动，它受到地球的万有引力充当向心力，用它运动周期表示向心力，由万有引力定律结合牛顿第二定律得：GMmr2=m?4π2rT2
∴地球的质量M=4π2r3GT2，其中r为地球与月球间的距离，故B正确．
C、人造卫星绕地球做匀速圆周运动，它受到地球的万有引力充当向心力，用它运动周期表示向心力，
由万有引力定律结合牛顿第二定律得：GMmr2=m?4π2rT2
又因T=2πrv，
∴地球的质量M=Tv32πG，因此，可求出地球的质量，故C正确．
D、地球表面的物体受到的地球的重力等于万有引力，即mg=GMmr2，因此，可求出地球的质量M=gr2G，故D正确．
故选BCD．

本题解析：

本题难度：一般

4、选择题  一些星球由于某种原因而发生收缩，假设该星球的直径缩小到原来的四分之一，若收缩时质量不变，则与收缩前相比（　　）
A．同一物体在星球表面受到的重力增大到原来的4倍
B．同一物体在星球表面受到的重力增大到原来的2倍
C．星球的第一宇宙速度增大到原来的4倍
D．星球的第一宇宙速度增大到原来的2倍

参考答案：A、忽略星球自转的影响，根据万有引力等于重力列出等式
GMmR2=mg
该星球的直径缩小到原来的四分之一，若收缩时质量不变，
所以同一物体在星球表面受到的重力增大到原来的16倍．故A、B错误．
C、第一宇宙速度是近星的环绕速度，根据万有引力提供向心力，列出等式
有GMmR2=mv2R，
v=

本题解析：

本题难度：简单

5、选择题  为了估算一个天体的质量需要知道绕该天体做匀速圆周运动的另一星球的条件是（引力常量G为已知）：①运转周期和轨道半径②质量和运转周期③轨道半径和环绕速度④环绕速度和质量（　　）
A．①或③
B．①或④
C．②或③
D．②或④

参考答案：研究卫星绕天体做匀速圆周运动，根据万有引力提供向心力，列出等式
GMmr2=m?来源:91考试网 91exam.org4π2rT2
M=4π2r3GT2，T为运转周期，r为轨道半径．故①正确．
研究卫星绕天体做匀速圆周运动，根据万有引力提供向心力，列出等式
GMmr2=mv2r
M=rv2G，r为轨道半径，v是环绕速度，故③正确．
在中心体质量的表达式中我们可以发现中心体质量与环绕体质量无关．
故选A．

本题解析：

本题难度：简单