1、计算题  如图A、B、C三个木块的质量均为m，置于光滑的水平面上，B、C之间有一轻质弹簧，弹簧的两端与木块接触而不固连，将弹簧压紧到不能再压缩时用细线把B和C紧连，使弹簧不能伸展以至于B、C可视为一个整体，现A以初速度V0沿BC的连线方向朝B运动，与B相碰并粘合在一起，以后细线突然断开，弹簧伸展，从而使C与A、B分离，已知C离开弹簧后的速度恰为V0，求
（1）A、B一起运动的速度；
（2）弹簧释放的势能。

参考答案：解：（1）设碰后A、B和C的共同速度的大小为v，由动量守恒定律得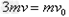
设C离开弹簧时，A、B的速度大小为v1，由动量守恒得
v1=0?
（2）设弹簧的弹性势能为EP，从细线断开到C与弹簧分开的过程中机械能守恒，有
?

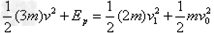本题解析：

本题难度：一般

2、简答题  大原子反应堆中，用石墨（碳）做减速剂使快中子变为慢中子，已知碳核的质量是中子质量的12倍，假设中子与碳核的碰撞是弹性的（即碰撞中不计能量损失），而且碰撞前碳核是静止的，
试求：（1）设碰撞前中子的动能为E0，问经过一次碰撞后，中子的动能损失多少？
（2）至少经过多少次碰撞，中子的动能才能少于10-6E0（lg13=1.114，lg11=1.041）？

参考答案：
（1）设中子的质量为m，速度为v0，碳核的质量为M0，二者碰撞后的速度分别为：v1、v，则
根据动量守恒定律和能量守恒定律得
mv0=mv1+Mv ①
12mv20=12mv21+12Mv2②
由①②可得：v1=-1113v0
碰撞一次，中子的动能损失为：△E=12mv20-12mv21=12mv20[1-(1113)2]=48169E0
（2）中子与碳核第一次碰撞后剩余的动能为：E1=12mv21=12m(-1113v0)2]=(1113)2E0
同理经过第二次碰撞后，中子剩余的动能为：E2=12mv22=12m(1113v1)2=(1113)2×2E0
…
第n次碰撞后中子剩余的动能为：En=12mv2n=12m(1113vn-1)2=(1113)2nE0=10-6E0
有(1113)2nE0=10-6E0，即(1113)2n=10-6
两边取对数可得：2n（lg11-lg13）=-6
得：n=41.1≈42次
答：
（1）设碰撞前中子的动能为E0，经过一次碰撞后，中子的动能损失是48169E0；
（2）至少经过42次碰撞，中子的动能才能少于10-6E0．

本题解析：

本题难度：简单

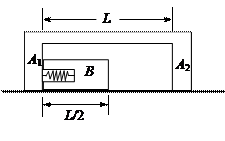
3、简答题  如图所示，滑块A1A2由轻杆连结成一个物体，其质量为M，轻杆长L．滑块B的质量为m，长L/2，其左端为一小槽，槽内装有轻质弹簧．开始时，B紧贴A，使弹簧处在压缩状态．今突然松开弹簧，在弹簧作用下整个系统获得动能Ek，弹簧松开后，便离开小槽并远离物体A1A2．以后B将在A1和A2之间发生无机械能损失的碰撞．假定整个系统都位于光滑的水平面上，求物块B的运动周期．

参考答案：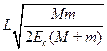

本题解析：设弹簧松开后A1A2物体与物体B的速度各为V和v，则有
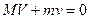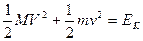? ①?? ②
解得，
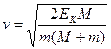
B和A碰撞前后? ③
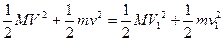? ④
联立③④式解得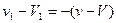? ⑤
即碰撞前后，B相对A1A2的速度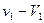的大小不变，只改变方向．
同理可证明，当B与A1碰撞后，也有同样的结果，即相对A1A2，B在以大小不变的相对速度作往返运动．运动的周期为．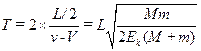

本题难度：一般

4、简答题  如图5-6所示浮动起重机从岸上吊起m=2t的重物。开始时浮吊起重杆OA与竖直方向成60°角，当转至杆与竖直方向成30°角时，求起重机的水平方向的位移。设浮吊质量为20t，起重杆长l=8m，水的阻力与杆重均不计。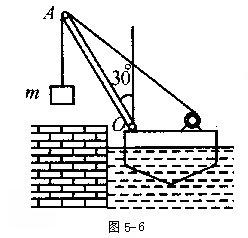

参考答案：起重机的水平向左的位移为0.266m

本题解析：浮吊与重物组成的系统水平方向不受外力，动量守恒且初总动量为零，为一人船模型，则：

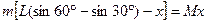
解得x=0.266m，即起重机的水平向左的位移为0.266m。

本题难度：简单

5、选择题  一个γ光子的能量为E，动量为P，射到一个静止的电子上，被电子反射回来，其动量大小变为P1，能量变为E1，电子获得的动量为P2，动能为E2则有
A．E1