1、计算题  如下图甲所示，一半径R=0.1m、竖直圆弧形光滑轨道，与斜面相切于B处，圆弧的最高点为M，斜面倾角θ=60°，t=0时刻，有一物块沿斜面上滑，其在斜面上运动的速度变化规律如图乙所示，物块质量m=lkg，若物块恰能到M点（取g=10m／s2）求：

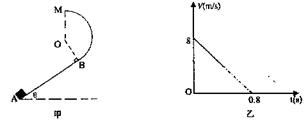
（1）物块经过B点时的速度VB；?
（2）物块在斜面上滑动的过程中摩擦力做功的平均功率。

参考答案：由题可知，圆弧圆心角应为120°（1分）
滑块从B到M上升的高度为R+Rcos60°（1分）
滑块恰好能过最高点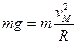，?（2分）
滑块从B到M的过程中，机械能守恒
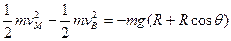（2分）
代入有关数据可得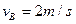?（1分）
（2）由图可知，滑块在斜面上滑动时，加速度大小为10m/s2（2分）
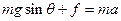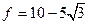?摩擦力?（2分）
平均速度为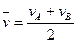=5m/s（1分）
所以摩擦力的平均功率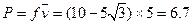w（2分）

本题解析：略

本题难度：一般

2、简答题  跳水运动是我国体育运动的优势项目，某运动员参加10m跳台的跳水比赛，如其质量为m=60kg，其体形可等效为长度L=1.0m，直径d=0.3m的圆柱体，不计空气阻力，运动员站立在跳台上向上跳起到达最高点时，他的重心离跳台台面的高度为1.3m，在从起跳到接触水面过程中完成一系列动作，入水后水的等效阻力F（未包含浮力）作用于圆柱体的下端面，F的数值随入水深度y变化的函数图象如图所示，该直线与F轴相交于F=2.5mg处，与y轴相交于y=h?（某一未知深度），已知水的密度ρ=1×103㎏/m3，根据以上的数据进行估算（g取10m/s2）．
（1）运动员起跳瞬间所做的功；
（2）运动员起跳瞬间获得的速度大小；
（3）运动员刚接触到水面瞬间的动能；
（4）运动员入水可以达到的最大深度h?（结果保留两位有效数字）．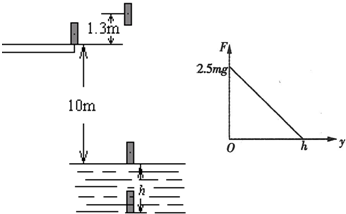

参考答案：（1）运用动能定理研究运动员站立在跳台上向上跳起到达最高点得：
运动员起跳瞬间所做的功为W，
W-mgh1=0-0
W=60×10×（1.3-0.5）=480J
（2）运动员起跳过程
W=12mv2-0?
v=4m/s
（3）运动员从起跳到刚接触水面，运用动能定理得：
mgh′=Ek′-12mv2
解得：运动员刚接触到水面瞬间的动能Ek′=6480J．
（4）运动员从刚接触水面到最深处
mgh-12×2.5mgh-12ρgVL-ρgV（h-L）=0-12mvˊ2
体积V=π（d2）2?L
解得：h=7.98m
答：（1）运动员起跳瞬间所做的功是480J；
（2）运动员起跳瞬间获得的速度大小是4m/s；
（3）运动员刚接触到水面瞬间的动能是6480J；
（4）运动员入水可以达到的最大深度是7.98 m

本题解析：

本题难度：一般

3、简答题  如图所示，一个质量为m的圆环套在一根固定的水平直杆上，环与杆的动摩擦因数为μ，现给环一个向右的初速度v0，如果环在运动过程中还受到一个方向始终竖直向上的力F的作用，已知F=kv（k为常数，v为速度），试讨论环在运动过程中克服摩擦力所做的功．（假设杆足够长）

参考答案：根据题意有对于小环的运动，根据环受竖直向上的拉力F与重力mg的大小分以下三种情况讨论：
（1）当mg=kv0时，即v0=mgk时，环做匀速运动，Wf=0，环克服摩擦力所做的功为零?
（2）当mg＞kv0时，即v0＜mgk时，环在运动过程中做减速运动，直至静止．由动能定理得环克服摩擦力所做的功为Wf=12mv20
（3）当mg＜kv0时，即v0＞mgk时，环在运动过程中先做减速运动，当速度减小至满足mg=kv时，即v=mgk时环开始做匀速运动．由动能定理得摩擦力做的功
Wf=12mv2-12mv20=m3g22k2-12mv20
环克服摩擦力所做的功为12mv20-m3g22k2
答：环在运动过程中克服摩擦力所做的功为：
（1）v0=mgk时，环做匀速运动，Wf=0，环克服摩擦力所做的功为零?
（2）v0＜mgk时，环克服摩擦力所做的功为Wf=12mv20
（3）v0＞mgk时，环克服摩擦力所做的功为12mv20-m3g22k2

本题解析：

本题难度：一般

4、简答题  ?如图所示是示波器的原理示意图．电子从灯丝发射出来，经电压为U1的电场加速后，通过加速极板A上的小孔O1射出，然后沿中心线O1O2进入M、N间的偏转电场，偏转电场的电压为U2，场强方向垂直于O1O2，电子离开偏转电场后，最终打在垂直于O1O2放置的荧光屏上的P点．已知电子的电荷量为e，平行金属板M、N间的距离为d，极板长为l，极板右端与荧光屏之间的距离为L，电子离开灯丝时的初速度可忽略，电子所受重力以及电子之间的相互作用力不计．
（1）若把P点到O2点的距离称为偏转距离Y，其偏转距离Y为多少？
（2）求电子即将到达P点时的动能．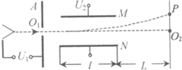

参考答案：（1）设电子到达O1时的速度为v，则
eU1=12mv2
设电子在偏转电场MN中运动的加速度为a，运动时间为t，则
h=12at2
a=eU2md
t=lv
解得：h=U2l24U1d
由：hY=l2l2+L
解得：Y=U2l24U1d(1+2Ll)
故偏转距离Y=U2l24U1d(1+2Ll)．
（2）由动能定理：eU1+eU2hd=EKP-0
得：EKP=eU1+eU22l24U1d2
故电子即将到达P点时的动能为eU1+eU22l24U1d2．

本题解析：

本题难度：一般

5、简答题  电子扩束装置由相邻的电子加速器、偏转电场和偏转磁场组成．偏转电场由两块水平平行放置的长为l相距为d的导体板组成，如图甲所示．大量电子（其重力不计，质量为m、电荷量为e）由静止开始，经加速电场加速后，连续不断地水平向右从两板正中间射入偏转电场．当两板不带电时，电子通过两板之间的时间均为2t0，当在两板间加如图乙所示的周期为2t0、最大值恒为U0的电压时，所有电子均可射出偏转电场，并射入垂直纸面向里的匀强磁场，最后打在磁场右侧竖直放置的荧光屏上．磁场的水平宽度为s，竖直高度足够大．求：
（1）加速电场的电压
（2）电子在离开偏转电场时的最大侧向位移；
（3）要使侧向位移最大的电子能垂直打在荧光屏上，匀强磁场的磁感应强度为多大？

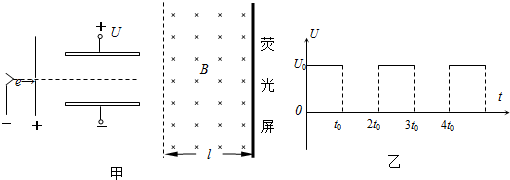
参考答案：（1）电子离开加速电场时的速度为 v0=l2t0
在加速电场中，由动能定理得 eU=12mv20
得U=ml28et20
（2）要使电子的侧向位移最大，应让电子从0、2t0、4t0…等时刻进入偏转电场
由牛顿第二定律得? eU0d=ma
类平抛运动过程侧向位移? y′1=12at20=eU0t202md，vy′=at?0=eU0t?0md
匀速直线运动侧向位移? y′2=vyt0=eU0t20md
故最大侧向位移y=y′1+y2=3eU0t202md
（3）设电子从偏转电场中射出时的偏向角为θ，要电子垂直打在荧光屏上，则电子在磁场中运动半径应为：R=s?sinθ
设电子从偏转电场中出来时的速度为v，垂直偏转极板的速度为vy，则电子从偏转电场中出来时的偏向角为：sinθ=vyvt
式中?vy=U0edmt?0
又Bev=mv2R
由上述四式可得：B=U0t0?ds
答：（1）加速电场的电压是ml28et20；
（2）电子在离开偏转电场时的最大侧向位移3eU0t202md；
（3）要使侧向位移最大的电子能垂直打在荧光屏上，匀强磁场的磁感应强度为U0t0ds．

本题解析：

本题难度：一般