1、单选题  将1～9个数字分别填入右边的九宫阵，使阵中每一行，每一列的三个数字之和均为15，其中的数字1可以填入阵中的_____位置。 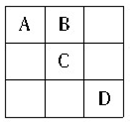A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点趣味数学问题解析根据九宫格的性质，正中间的位置必填5，排除C;A与D为对称位置，本质上是一样，均可排除。故正确答案为B。

2、单选题  某公司100名员工对甲、乙两名经理进行满意度评议，对甲满意的人数占全体参加评议的3/5，对乙满意的人数比甲的人数多6人，对甲乙都不满意的占满意人数的1/3多2人，则对甲乙都满意的人数是_____。
A: 36
B: 26
C: 48
D: 42
参考答案: D
本题解释:正确答案是D考点容斥原理问题解析对甲满意的人数为60人，对乙满意的人数为66人，设对甲、乙都满意的人数为X，则对甲、乙都不满意的人数为1/3X+2，由两集合容斥原理的推论公式可知，100-(1/3X+2)=60+66-X，解得X=42，故正确答案为D。两集合容斥原理推论公式：满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。

3、单选题  某实验室需购某种化工原料150千克，现在市场上原料按袋出售，有两种包装，一种是每袋45千克，价格为280元;另一种是每袋36千克，价格为240元，在满足需要的条件，最少要花费_____。
A: 960元
B: 1000元
C: 1040元
D: 1080元
参考答案: B
本题解释:正确答案是B考点其他解析要想花费最少，就要在购买的总重量尽可能接近150千克的情况下使总的价格最低，选项中的最低价为960元，960元只能购买4袋每袋为240元原料，此时总重量为4×36=144(千克)，小于150千克，不满足条件，排除A选项;B、C、D三个选项中的最低价为B选项1000元，1000元可以购买3袋每袋为240元的原料和1袋每袋为280元的原料，总重量为3×36+1×45=153(千克)，总重量接近150千克(满足实验室的需求)，并且在B、C、D三个选项中的最低价，故正确答案为B。

4、单选题  某单位招录了10名新员工，按其应聘成绩排名1到10，并用10个连续的四位自然数依次作为他们的工号，凑巧的是每个人的工号都能被他们的成绩排名整除，问排名第三的员工工号所有数字之和是多少_____。
A: 12
B: 9
C: 15
D: 18
参考答案: A
本题解释:正确答案是A考点多位数问题解析假设10个工号依次为N+1、N+2、……、N+10，由题意，N+A能够被A整除(A为1、2、……、10)，则N能够被A整除。于是N能够被1、2、……、10整除，因此N至少为1、2、……、10的最小公倍数，则在四位数上N最小为2520，可知此时第三位工号为2523，其数字和为12。故正确答案为A。秒杀技由题意第三位的工号加上6后为第九位的工号，因此能被9整除，也即第三位的工号数字之和加上6后能够被9整除，在四个选项中仅A符合。标签数字特性

5、单选题  如右图所示，△ABC是等腰直角三角形，AB=12，AD的长度是CD的2倍，四边形EBCD与△AED的面积之比为3：2，AE的长度是_____。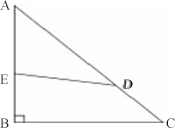A: 6.9
B: 7.1
C: 7.2
D: 7.4
参考答案: C
本题解释:正确答案是C考点几何问题解析四边形EBCD与三角形AED的面积之比为3：2，则三角形ABC与三角形AED的面积之比为5：2。已知AD的长度是CD的2倍，则AD的长度是AC的2/3。作DF垂直AB于点F，则DF=2/3BC(相似三角形原理)，三角形ABC的面积=1/2×AB×BC，三角形AED的面积=1/2×AE×DF=1/2×AE×2/3BC代入之前的比例式，可得AE=3/5AB=36/5=7.2。所以正确答案为C。