1、单选题  某矿井发生透水事故，且矿井内每分钟涌出的水量相等，救援人员调来抽水机抽水，如果用两台抽水机抽水，预计40分钟可抽完;如果用4台同样的抽水机，16分钟可抽完。为赢得救援时间，要在10分钟内抽完矿井内的水，那么至少需要抽水机_____。
A: 5台
B: 6台
C: 7台
D: 8台
参考答案: B
本题解释:正确答案是B考点牛吃草问题解析解析1：假定矿井原有水量为N，每分钟涌入的水量为n，根据题意可得N=(2-n)×40，N=(4-n)×16，解得n=2/3，N=160/3，因此要在10分钟内抽完矿井内的水需要抽水机为160/3÷10+2/3=6台。公式：在牛吃草模型背景下，公式为N=(牛数-x)×天数，其中N表示原有草量的存量，以牛数与天数的乘积来衡量;x表示专门吃新增加草量所需要的牛数。解析2：设每台抽水机每分钟抽水1个单位，那么，每分钟进水量为(2×40-4×16)÷(40-16)=2/3个单位，原来的积水量为2×40-(2/3)×40=160/3，那么10分钟内抽完水，需要[(160/3)+10×(2/3)]÷10=6台。故正确答案为B。标签赋值思想

2、单选题  两个相同的瓶子装满酒精溶液，一个瓶子中酒精与水的体积比是3∶1，另一个瓶子中酒精与水的体积比是4∶1，若把两瓶酒精溶液混合，则混合后的酒精和水的体积之比是多少?_____
A: 31∶9
B: 7∶2
C: 31∶40
D: 20∶11
参考答案: A
本题解释:正确答案是A考点其他解析设两个瓶子每个容量为20，第一个瓶子中酒精和水分别为15和5;另一个瓶子中酒精和水分别为16和4，混合后酒精和水体积比为(15+16)：(5+4)=31：9，故正确答案为A。秒杀技混合后酒精与水的比例显然介于3到4之间，只有选型A、B符合，而选项B显然是题目设置的陷阱选项(直接将数字相加)，因此只剩A项，故正确答案为A。标签赋值思想

3、单选题  某俱乐部中女会员的人数比男会员的一半少61人，男会员的人数比女会员的3倍多2人，问该俱乐部共有会员多少人?_____
A: 475人
B: 478人
C: 480人
D: 482人
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析设女会员有X人，男会员为Y人，则有0.5Y-61=X，3X+2=Y，解得X=120，Y=362，总人数为120+362=482。故正确答案为D。秒杀技由题目第一个条件可知会员总数加上61后能被3整除，也即加上1后能被3整除，仅选项D符合。标签数字特性

4、单选题  假设五个相异正整数的平均数是15，中位数是18，则此五个正整数中的最大数的最大值可能为：_____。
A: 35
B: 32
C: 24
D: 40
参考答案: A
本题解释:正确答案是A考点平均数问题解析五个相异正整数的平均数是15，故加和为15×5=75，为了让最大值尽可能大，则其他三个未知数要尽可能小，已知中位数为18，则比18小的两个数取1和2，比18大的取19，则最大值最大可能为75-18-1-2-19=35，故正确答案为A。

5、单选题  如下图所示，△ABC中DE∥BC，且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4cm，BC=24.5cm，AC=20cm。问△ADE的周长是多少?_____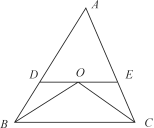A: 45.4cm
B: 45.1cm
C: 44.8cm
D: 44.5cm
参考答案: A
本题解释:正确答案是A考点几何问题解析BO是∠ABC的角平分线，则∠ABO=∠OBC，又DE∥BC，得∠OBC=∠BOD，因此△BOD是等腰三角形，有BD=OD，同理有CE=OE，因此△ADE的周长=AD+AE+DE=AB+AC=45.4(cm)。标签画图分析