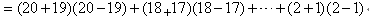1、单选题  如果5*2=5+6=11，6*3=6+7+8=21，那么1*9+2*9+3*9+…+9*9=_____。
A: 629
B: 729
C: 759
D: 829
参考答案: B
本题解释:参考答案:B
题目详解:根据题意，可知：5*2表示从5开始两个自然数相加;6*3表示从6开始的三个自然数相加;那么1*9=1+2+3+4+5+6+7+8+9，2*9=2+3+4+5+6+7+8+9+10，…9*9=9+10+11+12+13+14+15+16+17;分析，可知：1*9，2*9，…，9*9每组均有9个数字相加，且后面每一组里的9个数字均比前一组里的9个数字大1，即1*9，2*9，…，9*9构成公差为9，首项为1*9=1+2+…+9=45，项数为9的等差数列;故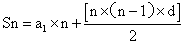

2、单选题  甲、乙两人在长30米的泳池内游泳，甲每分钟游37.5米，乙每分钟游52.5米，两人同时分别从泳池的两端出发，触壁后原路返回，如是往返。如果不计转向的时间，则从出发开始计算的1分50秒内两人共相遇了多少次?_____
A: 2
B: 3
C: 4
D: 5
参考答案: B
本题解释:正确答案是B考点行程问题解析解析1：题目的关键在于第一次相遇，两人游过长度之和为泳池长，之后每次相遇，都需要两人再游过两个泳池长。两人一起游一个泳池长，所需时间为30÷(37.5+52.5)×60=20(秒)，因此两人分别在20秒时、60秒时、100秒时相遇，共相遇3次。故正确答案为B。解析2：关键点同解析1。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165(米)，为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时，也即两人分别在合游1个、3个、5个泳池长时相遇，故共相遇3次。故正确答案为B。解析3：套用公式。先看迎面相遇，30×(2N-1)≤(37.5+52.5)×11/6，得N≤3.25，即有3次迎面相遇;再看追上相遇，30×(2N-1)≤(52.5-37.5)×11/6，得N≤23/24，即没有追及相遇。故总的相遇次数为3次。故正确答案为B。公式：两运动体从两端同时出发，相向而行，不断往返：第N次迎面相遇，两运动体路程和=全程×(2N-1);第N次追上相遇，两运动体路程差=全程×(2N-1)。标签公式应用

3、单选题  有两种电话卡：第一种每分钟话费0.3元，除此以外，无其他费用;第二种电话卡，每分钟0.2元，另有每月固定费用10元(无论拨打与否都要扣)。如果小王每月通话量不低于两个小时，则他办理哪种卡比较合算?_____
A: 第一种
B: 第二种
C: 两个卡一样
D: 无法判断
参考答案: B
本题解释:正确答案是B考点分段计算问题解析设小王每月通话量m分钟，则m>120，使用第一种电话卡费用为0.3×m，使用第二种电话卡费用为10+0.2m，因为0.3m-0.2m-10=0.1m-10>0.1×120-10>0，所以第一种电话卡费用更高。故正确答案为B。

4、单选题  将进货单价为90元的某商品按100元一个出售时，能卖出500个，已知这种商品如果每个涨价1元，其销售量就会减少10个,为了获得最大利润，售价应定为_____。
A: 120元
B: 110元
C: 130元
D: 150元
参考答案: A
本题解释:正确答案是A考点函数最值问题解析

5、单选题 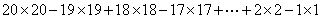 A: 210
B: 240
C: 273
D: 284
参考答案: A
本题解释:参考答案:A
题目详解:原式=(20×20-19×19)+(18×18-17×17)+…+(2×2-1×1)