1、单选题  有AB两个电脑显示器，已知旧显示器A的宽高比是4：3，新显示器B的宽高比例是16：9，若两个显示器面积相同，问B的宽与A的宽度比是_____。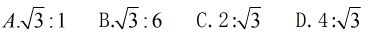A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析

2、单选题  一个班有50名学生，他们的名字都是由2个字或3个字组成的。将他们平均分为两组之后，两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5
B: 8
C: 10
D: 12
参考答案: C
本题解释:正确答案是C考点不定方程问题解析由题意可知，两组学生名字字数相差10，两边人数相同，即其中一组比另一组字数为3的人数多10人，则字数为2的人数少10人。故正确答案为C。

3、单选题  光明小学体育馆保管室的篮球和排球共30个，其比例为7:3，现购入排球x个后，排球占总数的40%，那么x=_____。
A: 5
B: 7
C: 10
D: 12
参考答案: A
本题解释:正确答案是A考点和差倍比问题解析根据篮球与排球的比例7：3可得，购入排球之前篮球和排球分别有21个和9个。购入x个排球后，排球占总数的40%，即篮球占总数的60%，则这时排球和篮球的总数为21÷60%=35个，因此购入的排球有14-9=5个。故正确答案为A。

4、单选题  某社团共有46人，其中35爱好戏剧，35人爱好体育，38人爱好写作，40人爱好收藏，这个社团至少有多少人以上四项活动都喜欢?_____
A: 5
B: 6
C: 7
D: 8
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析逆向考虑，分别考虑不喜欢其中某项活动的人数是多少。由题意可知，不喜欢戏剧的有11人，不喜欢体育的有16人，不喜欢写作的有8人，不喜欢收藏的有6人，只有当这四项集合相互没有交集时，四项活动都喜欢的人数才最少，因此最少人数为：46-(11+16+8+6)=5人，故正确答案为A。备注：要使四项都喜欢的人数最少，则需要使至少不喜欢其中某一项的人数应最多，而最多的情况是对应不喜欢其中某一项的四个集合之间不产生交叉。标签构造调整逆向考虑

5、单选题  有一种长方形小纸板，长为29毫米，宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形，问最少要多少块这样的小纸板_____
A: 197块
B: 192块
C: 319块
D: 299块
参考答案: C
本题解释:正确答案是C考点倍数约数问题解析本题可转化为求29与11的最小公倍数，即为29×11=319，则组成正方形的边长为319，从而可得组成正方形的小纸板数为319×319÷(29×11)=319(块)。故正确答案为C。