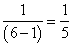1、单选题  某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分剐平均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人？_____
A: 36
B: 37
C: 39
D: 41
参考答案: D
本题解释:【答案】D。解析：假定每个钢琴教师带x个学生，每个拉丁舞教师带y个学生，则根据题意有：5x＋6y＝76。根据此方程，可知x必为偶数，而x与y均为质数，因此x＝2，代回可得y＝11。于是在学生人数减少后，还剩下学员为4×2＋3×11＝41个，故正确答案为D。

2、单选题  7643×2819－7644×2818的值是_____。
A: 4825
B: 4673
C: 5016
D: 5238
参考答案: A
本题解释:正确答案是A解析解析1：四个选项数字的尾数各不相同，采用尾数法，7643×2819的尾数为7，7644×2818的尾数为2，所以7643×2819－7644×2818的结果尾数为5，故正确答案为A。解析2：原式＝（7644×2819－2819）－7644×2818＝7644－2819＝4825，故正确答案为A。计算问题标签尾数法

3、单选题 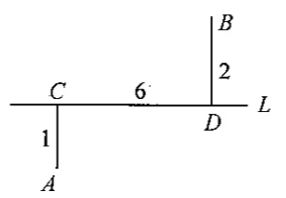 A: 2.75
B: 3.25
C: 2
D: 3
参考答案:
本题解释:参考答案:C
题目详解:由两点之间线段最短可知：连接AB，交公路L于点E，E点就是A、B两个村庄到此处处理垃圾都比较方便的地方。设CE距离为x：根据tanA=a/b可得：tanA=x/1=x，tanB=(6-x)/2=3-x/2;由于∠A=∠
B:故x=3-x/2，解得，x=2。即应建在离C处2公里。所以，选C。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)

4、单选题  若p和q为质数，且5p+3q=91，则p和q的值为：_____
A: 2，27
B: 3，19
C: 5，17
D: 17，2
参考答案: D
本题解释:参考答案
题目详解:5p+3q=91，∴p、q为一奇一偶，∵p和q为质数，∴p、q中必有一数为2，当p=2时，q=27，27为合数，故舍去，当q=2时，p=17。故p=17，q=2。故答案为：17，2。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性

5、单选题  甲、乙两位学生原计划每天自学的时间相同，若甲每天增加自学时间半小时，乙每天减少自学时间半小时，则乙自学6天的时间仅相当于甲自学一天的时间。问：甲、乙原计划每天自学多少分钟?_____
A: 42
B: 48
C: 56
D: 64
参考答案: A
本题解释:参考答案:A
题目详解:解法一：原来二者时间相同，现在甲每天增加自学时间半小时，乙每天减少自学时间半小时，甲比乙多自学一个小时，乙自学6天的时间仅相等于甲自学一天的时间，甲是乙的6倍，差倍问题。乙每天减少半小时后的自学时间为：