1、单选题  18名游泳运动员，有8名参加仰泳，有10名参加蛙泳，有12名参加自由泳，有4名既参加仰泳又参加蛙泳，有6名既参加蛙泳又参加自由泳，有5名既参加仰泳又参加自由泳，有2名这3个项目都参加。这18名游泳运动员中，只参加1个项目的有多少名?_____
A: 5 
B: 6 
C: 7 
D: 4
参考答案: B
本题解释: 【解析】B。利用文氏图可以迅速准确地求得答案。注意本题目的陷阱，18名运动员并不是都参加了项目。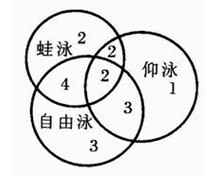

2、单选题  (2006国考B类)某工作组有12名外国人，其中6人会说英语，5人会说法语，5人会说西班牙语;有3人既会说英语又会说法语，有2人既会说法语又会说西班牙语，有2人既会说西班牙语又会说英语;有1人这三种语言都会说。则只会说一种语言的人比一种语言都不会说的人多：_____
A: 1人
B: 2人
C: 3人
D: 5人
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，设：

3、单选题  李森在一次村委会选举中，需2/3的选票才能当选，当统计完3/5的选票时，他得到的选票数已达到当选票数的3/4，它还需要得到剩下选票的几分之几才能当选?_____
A: 2500
B: 3115
C: 2225
D: 2550
参考答案: C
本题解释:正确答案是D考点倍数约数问题解析75=3×5×5，共6个约数，质因数每多个3则约数多3个，质因数每多个5则约数多2个，所以A=3×3×3×5×5=675，B=3×5×5×5×5=1875，A+B=2550，故正确答案为D。秒杀技由题意可知，A和B均能被3整除，则其和也能被3整除，仅选项D符合，故正确答案为D。

4、单选题  某种考试已举行了24次，共出了试题426道，每次出的题数有25题，或者16题，或者20题，那么其中考25题的有多少次?_____
A: 4 
B: 2 
C: 6 
D: 9
参考答案: B
本题解释:B【解析】 假设24次考试，每次16题，则共考16×24=384（道），比实际考题数少426-384=42（道），也就是每次考25题与每次考20题，共多考的题数之和为42道。而考25题每次多考25-16=9（道），考20题每次多考20-16=4（道）。这样有9×A+4×B=42，其中A表示考25题的次数，B表示考20题的次数。根据数的奇偶性可知，B无论是奇数还是偶数，4B总是偶数，那么9A也是偶数，因此A必定是偶数，且A不是2就是4。如果A=4，则9×4+4×B=42，B=1.5不合题意，应删去，所以考25道试题的次数是2次。

5、单选题  某S为自然数，被10除余数是9，被9除余数是8，被8除余数是7，已知100＜S＜1000，请问这样的数有几个？_____
A: 5  
B: 4 　 
C: 3 　 
D: 2
参考答案: D
本题解释:D。【解析】被N除余数是N-1，所以这个数字就是几个N的公倍数-1。10，9，8的公倍数为360n（n为自然数），因为100＜S＜1000，所以有两个数符合条件。