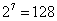1、单选题  100个自然数的和是20000，其中奇数的个数比偶数的个数多，那么偶数最多能有多少个?_____
A: 38
B: 40
C: 48
D: 49
参考答案: C
本题解释:参考答案:C
题目详解:依题意：“100个自然数的和是20000”，即和为偶数;又因为奇数的个数为偶数个，奇数的个数比偶数的个数多：所以最多有100÷2-2=48个偶数;所以，选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性

2、单选题  将60拆成10个质数之和，要求最大的质数尽可能小，那么其中最大的质数是_____。
A: 5
B: 9
C: 7
D: 11
参考答案: C
本题解释:参考答案:C
题目详解:依题意：最大的质数必大于5，否则10个质数之和将不大于60;又因为60分解质因数为：60=7+7+7+7+7+7+7+2+2：故其中最大的质数为7;所以，选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性

3、单选题  如果a，b均为质数，且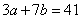A: 5
B: 6
C: 7
D: 8
参考答案: C
本题解释:参考答案:C
题目详解:首先，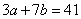

4、单选题  若p和q为质数，且5p+3q=91，则p和q的值为：_____
A: 2，27
B: 3，19
C: 5，17
D: 17，2
参考答案: D
本题解释:参考答案
题目详解:5p+3q=91，∴p、q为一奇一偶，∵p和q为质数，∴p、q中必有一数为2，当p=2时，q=27，27为合数，故舍去，当q=2时，p=17。故p=17，q=2。故答案为：17，2。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性

5、单选题  某年级150名同学准备选一名同学在教师节庆祝会上给老师献花。选举的方法是：让150名同学排成一排。由第一名开始报数，报奇数的同学落选退出队列，报偶数的同学站在原位不动，然后再从头报数，如此继续下去，最后剩下的一名当选。小胖非常想去，他在第一次排队时应该站在队列的什么位置才能被选中?_____
A: 64
B: 88
C: 108
D: 128
参考答案: D
本题解释:参考答案
题目详解:第一次报数，“从一开始报数，报奇数的同学退出队列”：故第一次报数，2的倍数原位不动;第二次报数：2的平方的倍数原位不动;第三次报数：2的立方的倍数原位不动;以此类推，到第7次：只剩下2的7次方的倍数原地不动，其余都退出，即排在