1、单选题  时钟指示2点15分，它的时针和分针所成的锐角是多少度?_____
A: 45度
B: 30度
C: 25度50分
D: 22度30分
参考答案: D
本题解释:参考答案
题目详解:时针每小时走30度，即每分钟时针走0.5度;分针每分钟走6度。假设12点钟时时针和分针为0度，则2点时时针在60度位置，再过15分钟的位置是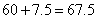

2、单选题  小强的爸爸比小强的妈妈大3岁，全家三口的年龄总和74岁，9年前这家人的年龄总和49岁，那么小强的妈妈今年多少岁？_____
A: 32
B: 33
C: 34
D: 35
参考答案: A
本题解释:【答案】A。解析：9年前全家年龄为49岁，而今年全家年龄为74岁每个人长9岁，49+27=76说明9年前小强未出生，小强的爸爸比小强妈妈大3岁，则妈妈9年前为23岁，今年32岁。因此，本题答案为A。

3、单选题  某工程项目由甲项目公司单独做，需4天完成，由乙项目公司单独做，需6天才能完成，甲、乙、丙三个公司共同做2天就可以完成，现因交工日期在即，需多公司合作，但甲公司因故退出，则由乙、丙公司合作完成此项目共需多少天?_____
A: 3
B: 4
C: 5
D: 6
参考答案: B
本题解释:正确答案是B考点工程问题解析由题意可设总工程量为12(4、6、2的公倍数)，所以甲的效率为12/4=3，乙的效率为12/6=2，丙的效率为12/2-3-2=1，所以若乙丙合作需要12÷(2+1)=4天。故正确答案为B。

4、单选题  某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，全部人员同时到达。已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?_____
A: 5.5小时
B: 5小时
C: 4.5小时
D: 4小时
参考答案: B
本题解释:参考答案:B
题目详解:根据题意，二队同时出发又同时到达，则二队步行的距离相等，乘车的距离也相等。设第一队乘车的距离是X，则步行的距离是100-X，那么第二队步行的距离也是100-X，汽车从第一队人下车到回来与第二队相遇所行驶的距离(即空车行使的距离)是：100-2×(100-X)=2X-100根据汽车从出发到与第二队相遇所用时间与第二队步行的时间相同，可列方程：[X+(2x-100)]÷40=(100-x)÷8解得，x=75。所用总时间为(以第一队为例)：乘车时间+步行时间=(75÷40)+(100-75)÷8=5小时所以，选B。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线一次相遇问题

5、单选题  一只船沿河顺水而行的航速为30千米/小时，已知按同样的航速在该河上顺水航行3小时和逆水航行5小时的航程相等，则此船在该河上顺水漂流半小时的航程为_____。
A: 1千米
B: 2千米
C: 3千米
D: 6千米
参考答案: C
本题解释:正确答案是C考点行程问题解析本题要理解问题是“顺水漂流半小时”，指的是半小时水流出多远，而不是船半小时的顺水航程。设顺水漂流速度为A千米/小时，则船静水航速为(30-A)千米/小时，逆水航速为(30-2A)千米/小时，根据题意得3×30=(30-2A)×5，解得A=6。因此船在该河上顺水漂流半小时的航程为3千米，故正确答案为C。