1、单选题 在1000以内,除以3余2,除以7余3,除以11余4的数有多少个?_____
A: 4
B: 5
C: 6
D: 7
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析同余问题,不符合“余同取余,和同加和,差同减差,最小公倍数做周期”的口诀,通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17,其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意:0≤231n+59≤1000,解得0≤n≤4。所以这样的数共有5个,故正确答案为B。口诀解释:余同取余,例如“一个数除以7余1,除以6余1,除以5余1”,可见所得余数恒为1,则取1,被除数的表达式为210n+1;和同加和,例如“一个数除以7余1,除以6余2,除以5余3”,可见除数与余数的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如“一个数除以7余3,除以6余2,除以5余1”,可见除数与余数的差相同,取此差4,被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。
2、单选题 有一批书要打包后邮寄,要求每包内所装书的册数都相同,用这批书的7/12打了14个包还多35本,余下的书连同第一次多的零头刚好又打了11包,这批书共有多少本?_____
A: 1000
B: 1310
C: 1500
D: 1820
参考答案: C
本题解释: C 解析: 由已知条件,全部书的7/12打14包还多35本,可知全部书的1/12打2包还多5本,即全部书的5/12打10包还多25本,而余下的是5/12加35本打11包。所以,(35+25)÷(11-10)=60本,1包是60本,这批书共有(14+11)×60=1500(本)。故本题正确答案为C。
3、单选题 已知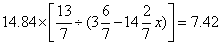 A:
A:  B:
B: 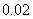 C:
C: 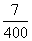 D:
D:  参考答案: D
参考答案: D
本题解释:参考答案
题目详解:观察可知14.84是7.42的2倍,则原式整理为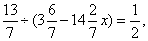
4、单选题 (2009吉林,第7题)甲、乙一起工作来完成一项工程,如果甲单独完成需要30天,乙单独完成需要24天,现在甲、乙一起合作来完成这项工程,但是乙中途被调走若干天,去做另一项任务,最后完成这项工程用了20天,问乙中途被调走_____天。
A: 8
B: 3
C: 10
D: 12
参考答案: D
本题解释:参考答案
题目详解:解法一:假设工程总量为“120”(30与24的最小公倍数),由题意易知:甲的工作效率为:
5、单选题 某招聘会在入场前若干分钟就开始排队,每分钟来的求职人数一样多,从开始入场到等候入场的队伍消失,同时开4个入口需30分钟,同时开5个入口需20分钟。如果同时打开6个入口,需多少分钟?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点牛吃草问题解析假定原有人数N人,每分钟新增人数Y人,则可得:N=(4-Y)×30,N=(5-Y)×20,解得Y=2,N=60。将6个入口代入,可得所需时间为60÷(6-2)=15(分钟)。故正确答案为D。公式:在牛吃草模型背景下,公式为N=(牛数-Y)×天数,其中N表示原有草量的存量,以牛数与天数的乘积来衡量;Y表示专门吃新增加草量所需要的牛数。