1、单选题  小雨把平时节省下来的全部1角的硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小雨所有的1角硬币合起来总共是多少钱?_____
A: 3元
B: 5元
C: 4元
D: 6元
参考答案: D
本题解释:正确答案是D考点计数模型问题解析解析1：由硬币可围成正三角形、正方形可知，硬币总数既是3的倍数又是4的倍数，即3、4的最小公倍数是12，结合选项只有6元(即60角)满足条件，故正确答案为D。解析2：设正方形每边个数为x，则三角形每边个数为x+5，因此有4(x-1)=3(x+5-1)，解得x=16。因此硬币总个数为4×(16-1)=60，也即硬币合计6元。故正确答案为D。标签最小公倍数数字特性

2、单选题  某专业有学生50人，现开设有甲、乙、丙三门选修课。有40人选修甲课程，36人选修乙课程，30人选修丙课程，兼选甲、乙两门课程的有28人，兼选甲、丙两门课程的有26人，兼选乙、丙两门课程的有24人，甲、乙、丙三门课程均选的有20人，问三门课程均未选的有多少人?_____
A: 1人
B: 2人
C: 3人
D: 4人
参考答案: B
本题解释:正确答案是B考点容斥原理问题解析设选修甲课程的为集合A，选修乙课程的为集合B，选修丙课程的为集合C，根据三集合容斥原理公式：A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C，可得A∪B∪C=40+36+30-28-26-24+20=48，即至少选一门课的有48人，因此三门课程均未选的有：50-48=2，故选择B选项。秒杀技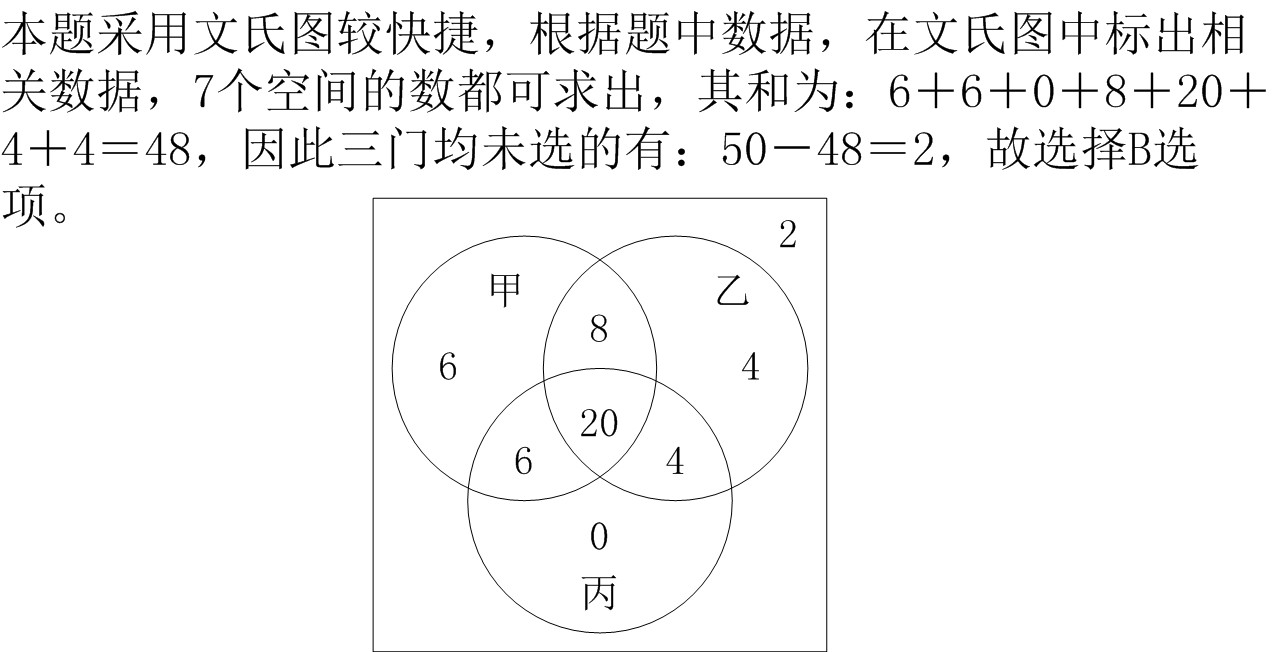

3、单选题  有一批资料，甲机单独复印需11时，乙机单独复印需13时，当甲乙两台复印机同时复印时，由于相互干扰，每小时两台共少印28张，现在两台复印机同时复印了6小时15分钟才完成，那么这批资料共有多少张？_____
A: 2860
B: 3146
C: 3432
D: 3575
参考答案: D
本题解释:【答案】D。解析：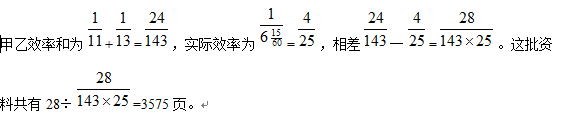

4、单选题  有两个工程队完成一项工程，甲队每工作6天后休息1天，单独做需要76天完工;乙队每工作5天后休息2天，单独做需要89天完工，照这样计算，两队合作，从1998年11月29日开始动工，到1999年几月几日才能完工?_____
A: 1月9日
B: 1月10日
C: 1月11日
D: 1月8日
参考答案: D
本题解释:参考答案
题目详解:根据题意，可知：甲单独做了76天完工，因为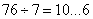

5、单选题  两港相距560千米，甲船往返两港需105小时，逆流航行比顺流航行多用了35小时。乙船的静水速度是甲船的静水速度的2倍，那么乙船往返两港需要多少小时?_____
A: 24
B: 20
C: 28
D: 48
参考答案: D
本题解释:参考答案:.D
题目详解:甲船往返航行的时间分别是：